
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,\Leftrightarrow\left\{{}\begin{matrix}1-4m=-\dfrac{1}{2}\\m-2\ne3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{3}{8}\\m\ne5\end{matrix}\right.\Leftrightarrow m=\dfrac{3}{8}\\ b,\Leftrightarrow1-4m>0\Leftrightarrow m< \dfrac{1}{4}\\ c,\Leftrightarrow x=\dfrac{1}{2};y=0\Leftrightarrow\dfrac{1}{2}\left(1-4m\right)=2-m\Leftrightarrow1-4m=4-2m\\ \Leftrightarrow m=-\dfrac{3}{2}\)




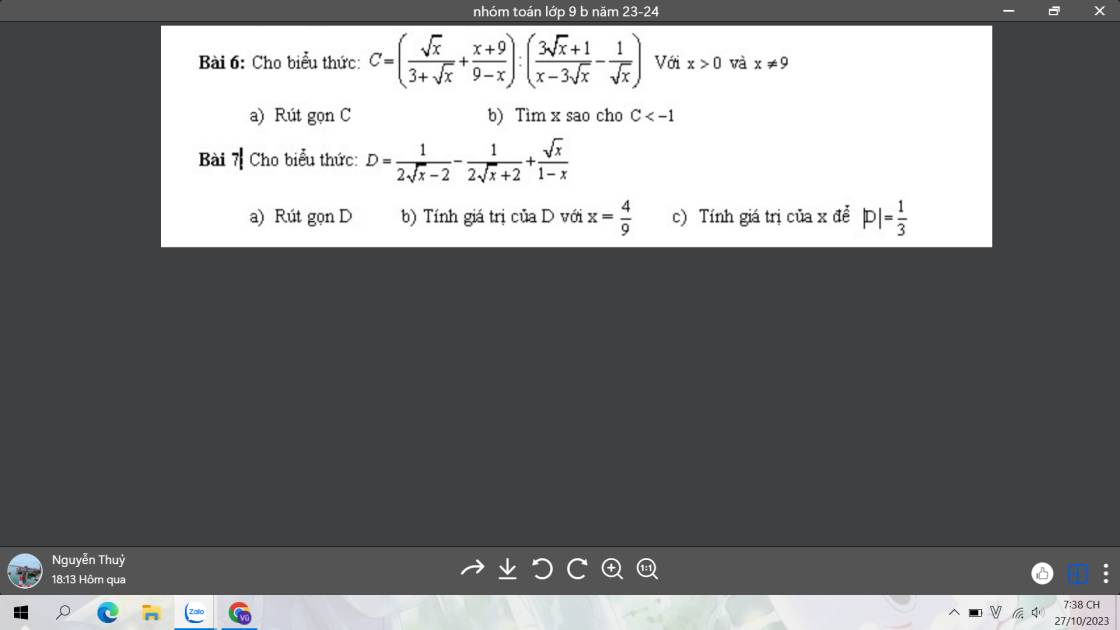
7:
a: ĐKXĐ: x>=0; x<>1
\(D=\dfrac{1}{2\sqrt{x}-2}-\dfrac{1}{2\sqrt{x}+2}+\dfrac{\sqrt{x}}{1-x}\)
\(=\dfrac{1}{2\left(\sqrt{x}-1\right)}-\dfrac{1}{2\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}+1-\sqrt{x}+1-2\sqrt{x}}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{-2\left(\sqrt{x}-1\right)}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{-1}{\sqrt{x}+1}\)
b: Khi x=4/9 thì \(D=\dfrac{-1}{\dfrac{2}{3}+1}=-1:\dfrac{5}{3}=-\dfrac{3}{5}\)
c: |D|=1/3
=>D=-1/3 hoặc D=1/3
=>\(\left[{}\begin{matrix}\dfrac{-1}{\sqrt{x}+1}=\dfrac{-1}{3}\\\dfrac{-1}{\sqrt{x}+1}=\dfrac{1}{3}\left(loại\right)\end{matrix}\right.\)
=>\(\sqrt{x}+1=3\)
=>\(\sqrt{x}=2\)
=>x=4
6:
a: \(C=\left(\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{x+9}{9-x}\right):\left(\dfrac{3\sqrt{x}+1}{x-3\sqrt{x}}-\dfrac{1}{\sqrt{x}}\right)\)
\(=\dfrac{\sqrt{x}\left(3-\sqrt{x}\right)+x+9}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}:\dfrac{3\sqrt{x}+1-\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{3\sqrt{x}-x+x+9}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}\cdot\dfrac{-\sqrt{x}\left(3-\sqrt{x}\right)}{2\sqrt{x}+4}\)
\(=\dfrac{3\left(\sqrt{x}+3\right)}{3+\sqrt{x}}\cdot\dfrac{-\sqrt{x}}{2\sqrt{x}+4}=\dfrac{-3\sqrt{x}}{2\sqrt{x}+4}\)
b: C<-1
=>C+1<0
=>\(\dfrac{-3\sqrt{x}+2\sqrt{x}+4}{2\sqrt{x}+4}< 0\)
=>\(-\sqrt{x}+4< 0\)
=>\(-\sqrt{x}< -4\)
=>\(\sqrt{x}>4\)
=>x>16
\(C=\left(\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{x+9}{9-x}\right):\left(\dfrac{3\sqrt{x}+1}{x-3\sqrt{x}}-\dfrac{1}{\sqrt{x}}\right)\\ =\left(\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{x+9}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}\right):\left(\dfrac{3\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-3\right)}-\dfrac{1}{\sqrt{x}}\right)\\ =\left(\dfrac{\sqrt{x}\left(3-\sqrt{x}\right)}{\left(3+\sqrt{x}\right)\left(3-\sqrt{x}\right)}+\dfrac{x+9}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}\right):\left(\dfrac{3\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-3\right)}-\dfrac{\sqrt{x}-3}{\sqrt{x}\left(\sqrt{x}-3\right)}\right)\\ =\dfrac{3\sqrt{x}-x+x+9}{\left(3+\sqrt{x}\right)\left(3-\sqrt{x}\right)}:\dfrac{3\sqrt{x}+1-\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{3\sqrt{x}+9}{\left(3+\sqrt{x}\right)\left(3-\sqrt{x}\right)}\cdot\dfrac{-\sqrt{x}\left(3-\sqrt{x}\right)}{2\sqrt{x}+4}\\ =\dfrac{3\left(\sqrt{x}+3\right)}{\left(3+\sqrt{x}\right)\left(3-\sqrt{x}\right)}\cdot\dfrac{-\sqrt{x}\left(3-\sqrt{x}\right)}{2\sqrt{x}+4}\\ =\dfrac{-3\sqrt{x}}{2\sqrt{x}+4}\)
Để `C < -1` Ta có :
\(\dfrac{-3}{2\sqrt{x}+4}< -1\\ \Leftrightarrow\dfrac{-3}{2\sqrt{x}+4}+1< 0\\ \Leftrightarrow\dfrac{-3}{2\sqrt{x}+4}+\dfrac{2\sqrt{x}+4}{2\sqrt{x}+4}< 0\\ \Leftrightarrow-3+2\sqrt{x}+4< 0\\ \Leftrightarrow2\sqrt{x}+1< 0\\ \Leftrightarrow2\sqrt{x}< -1\\ \Leftrightarrow\sqrt{x}< -\dfrac{1}{2}\\ \Leftrightarrow x< \dfrac{1}{4}\)

Đề sai rồi vì `P>0AAx>=0,x ne 1/2` mà phải tìm để `P<=0` nên nhất thiết mẫu là `2sqrtx-1` mặt khác còn lý do nữa là `x ne 1/2` mà không phải là `1/4` nên mình vẫn băn khoăn nhưng lý do đầu có vẻ thuyết phục hơn và sửa lại là `x ne 1/4` nhé!
`|P|>=P`
Mà `|P|>=0`
`=>P<=0`
`<=>(sqrtx+2)/(2sqrtx-1)<=0`
Mà `sqrtx+2>=2>0AAx>=0`
`<=>2sqrtx-1<0`
`<=>2sqrtx<1`
`<=>sqrtx<1/2`
`<=>x<1/4`
Vậy với `0<=x<1/4` thì `|P|>=P.`


 Mn giúp mik với,bh mik đang cần gấp lắm 19h30 mik phải có bài r nên mn giúp mik với
Mn giúp mik với,bh mik đang cần gấp lắm 19h30 mik phải có bài r nên mn giúp mik với 

 giúp mik với mn ơi mik đg cần gấp
giúp mik với mn ơi mik đg cần gấp

A B C M H K I
a/
Ta có A và M cùng nhìn BK dưới 1 góc vuông => A và M nằm trên đường tròn đường kính BK => ABMK là tứ giác nội tiếp đường tròn đường kính BK
Xét \(\Delta AMC\) và \(\Delta BKC\) có
\(\widehat{ACB}\) chung
\(\widehat{KBC}=\widehat{MAC}\) (góc nội tiếp đường tròn cùng chắn cung KM)
\(\Rightarrow\Delta BKC\) đồng dạng với \(\Delta AMC\) (g.g.g)
Xét tg vuông AHM có
HM=HA => tg AHM vuông cân tại H \(\Rightarrow\widehat{AMB}=45^o\)
Ta có \(\widehat{AKB}=\widehat{AMB}=45^o\) (góc nội tiếp đường tròn cùng chắn cung AB)
Xét tg vuông ABK có
\(\widehat{ABK}=90^o-\widehat{AKB}=90^o-45^o=45^o\)
\(\Rightarrow\widehat{ABK}=\widehat{AKB}=45^o\)=> tg ABK vuông cân tại A => AB=AK
\(\Rightarrow BK=\sqrt{AB^2+AK^2}=\sqrt{AB^2+AB^2}=AB\sqrt{2}\) (Pitago)
b/
Xét tg vuông cân ABK có
IB=IK (gt) => AI là trung tuyến => \(AI\perp BK\) (trong tg cân đường trung tuyến xp từ đỉnh đồng thời là đường cao)
=> I và H cùng nhìn AB dưới 1 góc vuông => ABHI là tứ giác nội tiếp
\(\Rightarrow\widehat{AHI}=\widehat{ABK}\) (góc nội tiếp cùng chắn cung AI)
Mà \(\widehat{ABK}=45^o\left(cmt\right)\Rightarrow\widehat{AHI}=45^o\)