Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 4:
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Vậy: BC=10cm
a) Xét ΔABC có BD là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{DA}{DC}=\dfrac{BA}{BC}\)(Tính chất tia phân giác của tam giác)
hay \(\dfrac{DA}{DC}=\dfrac{6}{10}=\dfrac{3}{5}\)

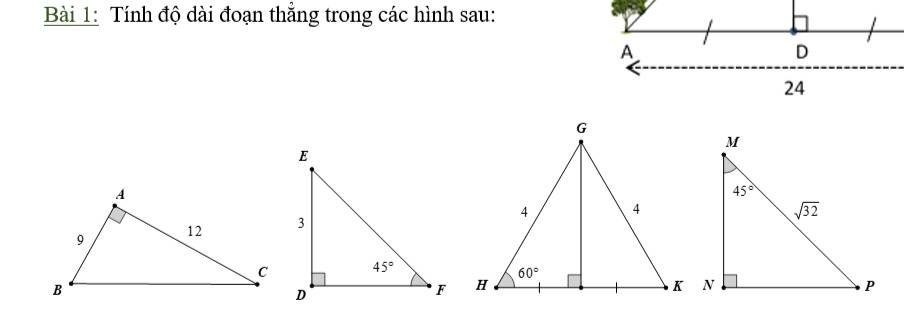
3: ΔGHK cân tại G có góc H=60 độ
nên ΔGHK đều
=>HK=GH=4
4: Xét ΔMNP vuông tại N có góc M=45 độ
nên ΔMNP vuông cân tại N
=>\(NP=NM=\sqrt{\dfrac{MP^2}{2}}=4\left(cm\right)\)

a: Xét tứ giác ABNC có
O là trung điểm của AN
O là trung điểm của BC
Do đó: ABNC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABNC là hình chữ nhật

$ĐKXĐ : x \neq 2, x \neq -2$
Ta có : $1+\dfrac{2}{x-2} = \dfrac{2x^2}{x^2-4}$
$\to \dfrac{x^2-4+2.(x+2)}{(x-2).(x+2)} = \dfrac{2x^2}{(x-2).(x+2)}$
$\to x^2-4+2.(x+2) = 2x^2$
$\to x^2 -2x - 8 = 0 $
$\to (x-4).(x+2) = 0 $
$\to x = 4$ ( Do $x \neq -2, 2$ )
Vậy \(S=\left\{4\right\}\)

\(=\left(x-5\right)^2-4y^2=\left(x-5-2y\right)\left(x-5+2y\right)\)



2x - | 6x - 7 | = -x + 8
* x > 0
Phương trình trở thành : 2x - 6x - 7 = -x + 8
<=> 2x - 6x + x = 8 + 7
<=> -3x = 15
<=> x = -5 ( không tmđk vì < 0 )
* x < 0
Phương trình trở thành : 2x - (-6x - 7) = -x + 8
<=> 2x + 6x + 7 = -x + 8
<=> 2x + 6x + x = 8 - 7
<=> 9x = 1
<=> x = 1/9 ( không tmđk vì > 0 )
Vậy phương trình vô nghiệm
Bài làm
~ Bài bạn Rin thiếu ngoặc khi xét biểu thức nếu vào phương trình đầu ~
*Nếu 6x - 7 > 0 <=> x > 7/6
----> | 6x - 7 | = 6x - 7
=> Phương trình: 2x - ( 6x - 7 ) = -x + 8
<=> 2x - 6x + 7 = -x + 8
<=> -4x + 7 + x - 8 = 0
<=> -3x - 1 = 0
<=> -3x = 1
<=> x = -1/3 ( Không thỏa mãn )
*Nếu 6x - 7 < 0 <=> x > 7/6
----> | 6x - 7 | = -( 6x - 7 ) = 7 - 6x
=> Phương trình: 2x - ( 7 - 6x ) = -x + 8
<=> 2x - 7 + 6x + x - 8 = 0
<=> 9x - 15 = 0
<=> x = 15/9 ( Thỏa mãn )
Vậy x = 15/9 là nghiệm phương trình.

\(\left(8x+5\right)\left(8x+7\right)\left(8x+6\right)^2=72\)
Đặt \(8x+5=t\left(t\ge0\right)\)
\(t\left(t+2\right)\left(t+1\right)^2-72=0\)
\(\Leftrightarrow t\left(t+1\right)\left(t+2\right)\left(t+1\right)-72=0\)
\(\Leftrightarrow\left(t^2+t\right)\left(t^2+3t+2\right)-72=0\)
\(\Leftrightarrow t^4+3t^3+2t^2+t^3+3t^2+2t-72=0\)
\(\Leftrightarrow t^4+4t^3+5t^2+2t-72=0\)
\(\Leftrightarrow\left(t^2+2t+9\ne0\right)\left(t+4\right)\left(t-2\right)=0\Leftrightarrow t=-4;2\)
hay \(8x+5=-4\Leftrightarrow x=-\frac{9}{8}\)( trường hợp 1 )
\(8x+5=2\Leftrightarrow x=-\frac{3}{8}\)( trưởng hợp 2 )
Vậy tập nghiệm của phương trình là S = { -9/8 ; -3/8 }
\(\left(8x+5\right)\cdot\left(8x+7\right)\cdot\left(8x+6\right)^2=72\)
Đặt \(t=8x+6\)
\(Pt\Leftrightarrow\left(t-1\right)\left(t+1\right)t^2-72=0\)
\(\Leftrightarrow\left(t^2-1\right)t^2-72=0\Leftrightarrow t^4-t^2-72=0\)
\(\Leftrightarrow\left(t^2-9\right)\left(t^2+8\right)=0\Leftrightarrow\orbr{\begin{cases}t^2=9\\t^2=-8\end{cases}\Leftrightarrow\orbr{\begin{cases}t=3\\t=-3\end{cases}}}\)
\(\Leftrightarrow\orbr{\begin{cases}8x+6=3\\8x+6=-3\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-\frac{3}{8}\\x=-\frac{9}{8}\end{cases}}}\)
Vậy....