K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 3 2022
Gọi x là qđ AB (km)
Vận tốc đi là \(25\left(\dfrac{km}{h}\right)\)
Vận tốc về là \(30\left(\dfrac{km}{h}\right)\)
Thời gian đi là \(\dfrac{x}{25}\left(h\right)\)
Thời gian về là \(\dfrac{x}{30}\left(h\right)\)
20p = 1/3(h)
Do thời gian về ít hơn lúc đi là 20p nên ta có
\(\dfrac{x}{25}-\dfrac{x}{30}=\dfrac{1}{3}\\ \Leftrightarrow30x-25x=\dfrac{1}{3}\\ \Leftrightarrow5x=\dfrac{1}{3}\\ \Leftrightarrow x=15\)
21 tháng 3 2022
Cách giải đây nhé!
Gọi thời gian lúc đi là x(x>0) (h)
Đổi 20 phút = 1/3 giờ
Do thời gian về ít hơn thời gian đi là 20 phút nên thời gian lúc về là x−1/3
Do quãng đường không đổi nên ta có phương trình :
25x= 30(x−1/3)
⇔ 25x= 30x−10
⇔ −5x= −10
5 tháng 8 2023
a: A=x^2+4x+4+5
=(x+2)^2+5>=5
Dấu = xảy ra khi x=-2
b: =3/2(x^2+2/3x+2/3)
=3/2(x^2+2*x*1/3+1/9+5/9)
=3/2(x+1/3)^2+15/18>=15/18=5/6
Dấu = xảy ra khi x=-1/3
e: =x^2-2x+1+4
=(x-1)^2+4>=4
Dấu = xảy ra khi x=1
f: =2(x^2-3x)
=2(x^2-3x+9/4-9/4)
=2(x-3/2)^2-9/2>=-9/2
Dấu = xảy ra khi x=3/2
h: =-(x^2-4x-3)
=-(x^2-4x+4-7)
=-(x-2)^2+7<=7
Dấu = xảy ra khi x=2
PT
20 tháng 3 2022
a) x(4x + 2) = 4x2 - 14
⇔ 4x2 + 2x = 4x2 - 14
⇔ 4x2 - 4x2 + 2x = -14
⇔ 2x = -14
⇔ x = -7
Vậy tập nghiệm S = ......
b) (x2 - 9)(2x - 1) = 0
⇔ x2 - 9 = 0 hoặc 2x - 1 = 0
⇔ x2 = 9 hoặc 2x = 1
⇔ x = 3 hoặc -3 hoặc x = \(\dfrac{1}{2}\)
Vậy .......
c) \(\dfrac{3}{x-2}\) + \(\dfrac{4}{x+2}\) = \(\dfrac{x-12}{x^2-4}\)
⇔ \(\dfrac{3}{x-2}\) + \(\dfrac{4}{x+2}\) = \(\dfrac{x-12}{\left(x-2\right)\left(x+2\right)}\)
ĐKXĐ: x - 2 ≠ 0 và x + 2 ≠ 0
⇔ x ≠ 2 và x ≠ -2MSC (mẫu số chung): (x - 2)(x + 2)Quy đồng mẫu hai vế và khử mẫu ta được:3x + 6 + 4x - 8 = x - 12⇔ 3x + 4x - x = 8 - 6 - 12⇔ 6x = -10⇔ x = \(-\dfrac{5}{3}\) (nhận)Vậy ........
6 tháng 3 2023
Bài 2:
Hình 3:
Xét ΔABC có AD là phân giác
nên x/3,5=7,2/4,5
=>x/3,5=1,8
=>x=6,3
Hình 4:
Xet ΔABC có MN//BC
nên 6/3=4/x
=>4/x=2
=>x=2
KV
6 tháng 3 2023
Bài 5
a) Ta có:
AB/A'B' = 6/4 = 3/2
AC/A'C' = 9/6 = 3/2
BC/B'C' = 12/8 = 3/2
⇒AB/A'B' = AC/A'C' = BC/B'C' = 3/2
⇒∆ABC ∽ ∆A'B'C' (c-c-c)
b) Do ∆ABC ∽ ∆A'B'C' (c-c-c)
⇒∠A = ∠A' = 100⁰
∠B = ∠B' = 44⁰
⇒∠C = 180⁰ - (∠A + ∠B)
= 180⁰ - (100⁰ + 44⁰)
= 36⁰
c) Tỉ số chu vi của ∆ABC và ∆A'B'C' là:
(AB + AC + BC)/(A'B' + A'C' + B'C')
= (6 + 9 + 12)/(4 + 6 + 8)
= 27/18
= 3/2
PL
3
30 tháng 8 2021
a)\(5x^2.\left(10x^4-5x^3+2\right)=50x^6-25x^5+10x^2\)
b) \(\left(x^2-5x+3\right).\left(-5x\right)=-5x^3+25x^2-15x\)
c) \(\left(5x-2y\right)\left(x^2-xy+1\right)=5x^3-5x^2y+5x-2x^2y+2xy^2-2y\\ =5x^3-7x^2y+2xy^2+5x-2y\)
d) \(\left(3x-2\right)\left(9x^2+6x-4\right)\\ =27x^3+18x^2-12x-18x^2-12x+8=27x^3+8\)
30 tháng 8 2021
a) \(5x^2\left(10x^4-5x^3+2\right)=50x^6-25x^5+10x^2\)
b) \(\left(x^2-5x+3\right)\left(-5x\right)=-5x^3+25x^2-15x\)
c) \(\left(5x-2y\right)\left(x^2-xy+1\right)=5x^3-5x^2y+5x-2x^2y+2xy^2-2y=5x^3-7x^2y+2xy^2+5x-2y\)
d) \(\left(3x-2\right)\left(9x^2+6x-4\right)=27x^3+18x^2-12x-18x^2-12x+8=27x^3-24x+8\)
MN
6
30 tháng 7 2021
Bài cuối mình không thấy rõ đề nhưng mình đoán là thế này bạn nhé.
NT
1
VD
21 tháng 3 2022
a, Áp dụng định lý Ta-lét ta có:
\(\dfrac{AD}{DB}=\dfrac{AE}{EC}\Rightarrow\dfrac{4}{x}=\dfrac{5}{10}\Rightarrow x=4:\dfrac{1}{2}\Rightarrow x=8\)
Áp dụng hệ quả định lý Ta-lét ta có:
\(\dfrac{AE}{AC}=\dfrac{DE}{BC}\Rightarrow\dfrac{5}{15}=\dfrac{6}{y}\Rightarrow y=6:\dfrac{1}{3}\Rightarrow y=18\)
b, Áp dụng định lý phân giác ta có:
\(\dfrac{DB}{DC}=\dfrac{AB}{AC}\Rightarrow\dfrac{5}{6}=\dfrac{10}{x}\Rightarrow x=10:\dfrac{5}{6}\Rightarrow x=12\)
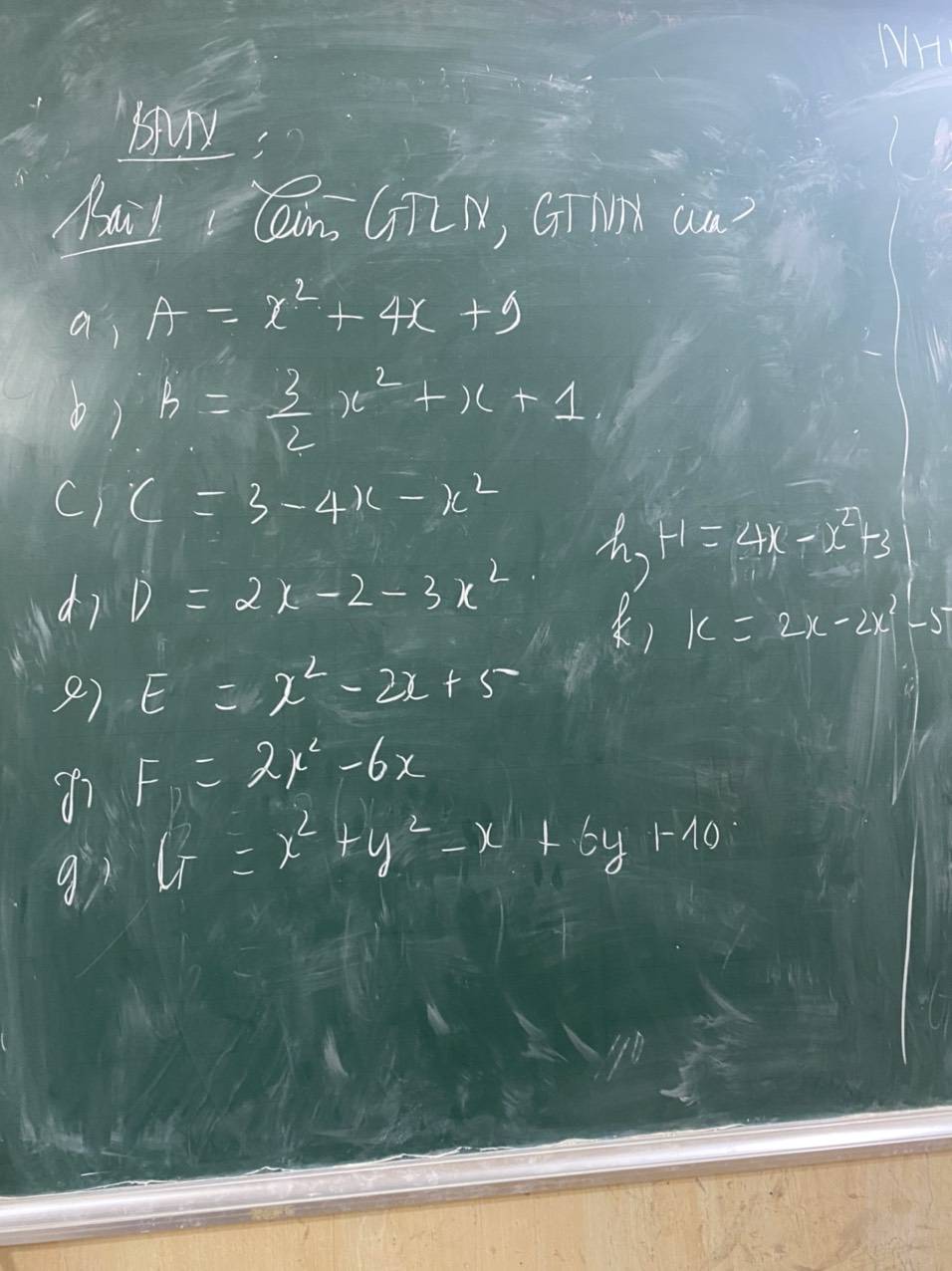
Bài toán đâu vậy bn
bài đâu bạn