
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: A=-1/2*xy^3*4x^2y^2=-2x^3y^5
Bậc là 8
Phần biến là x^3;y^5
Hệ số là -2
2:
a: P(x)=3x+4x^4-2x^3+4x^2-x^4-6
=3x^4-2x^3+4x^2+3x-6
Q(x)=2x^4+4x^2-2x^3+x^4+3
=3x^4-2x^3+4x^2+3
b: A(x)=P(x)-Q(x)
=3x^4-2x^3+4x^2+3x-6-3x^4+2x^3-4x^2-3
=3x-9
A(x)=0
=>3x-9=0
=>x=3


Bài 2 :
\(M=\left(-6x^2y\right)\left(-\dfrac{2}{3}xy^2\right)^2=\left(-6x^2y\right)\left(\dfrac{4}{9}x^2y^4\right)=-\dfrac{8}{3}x^4y^5\)
hệ số : -8/5 ; biến x^4y^5 ; bậc 5
b, Thay x = -1 ; y = 2 ta được
\(=-\dfrac{8}{3}.1.32=-\dfrac{256}{3}\)
Bài 4 :
a, \(M=\left(-\dfrac{3}{4}x^4y\right)\left(\dfrac{2}{9}x^2y^2\right)=-\dfrac{1}{6}x^6y^3\)
b, phần hệ số -1/6
phần biến x^6y^3
bậc 6

\(=\dfrac{5\cdot2^{30}\cdot3^{18}-3^{20}\cdot2^{29}}{5\cdot2^{29}\cdot3^{32}-7\cdot2^{29}\cdot3^{18}}\)
\(=\dfrac{2^{29}\cdot3^{18}\left(5\cdot2-3^2\right)}{2^{29}\cdot3^{18}\left(5\cdot3^{14}-7\right)}=\dfrac{1}{5\cdot3^{14}-7}\)


Bài 6:
a: Đặt 2x+3=0
=>2x=-3
hay x=-3/2
b: Đặt (x+1)(x-2)=0
=>x+1=0 hoặc x-2=0
=>x=-1 hoặc x=2
c: Đặt 2x2+4x=0
=>2x(x+2)=0
=>x=0 hoặc x=-2

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
b) Xét ΔABC có AB<AC<BC(3cm<4cm<5cm)
mà góc đối diện với cạnh AB là \(\widehat{ACB}\)
và góc đối diện với cạnh AC là \(\widehat{ABC}\)
và góc đối diện với cạnh BC là \(\widehat{BAC}\)
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
Xét ΔABC có
HB là hình chiếu của AB trên BC
HC là hình chiếu của AC trên BC
AB<AC
Do đó: HB<HC
c) Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD(gt)
Do đó: ΔCAB=ΔCAD(hai cạnh góc vuông)
Suy ra: CB=CD(hai cạnh tương ứng)
Xét ΔCBD có CB=CD(cmt)
nên ΔCBD cân tại C(Định nghĩa tam giác cân)

Bài 3:
Áp dụng tc dtsnb:
\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+2y-z}{5+3\cdot2-4}=\dfrac{63}{7}=9\\ \Rightarrow\left\{{}\begin{matrix}x=45\\y=27\\z=36\end{matrix}\right.\)



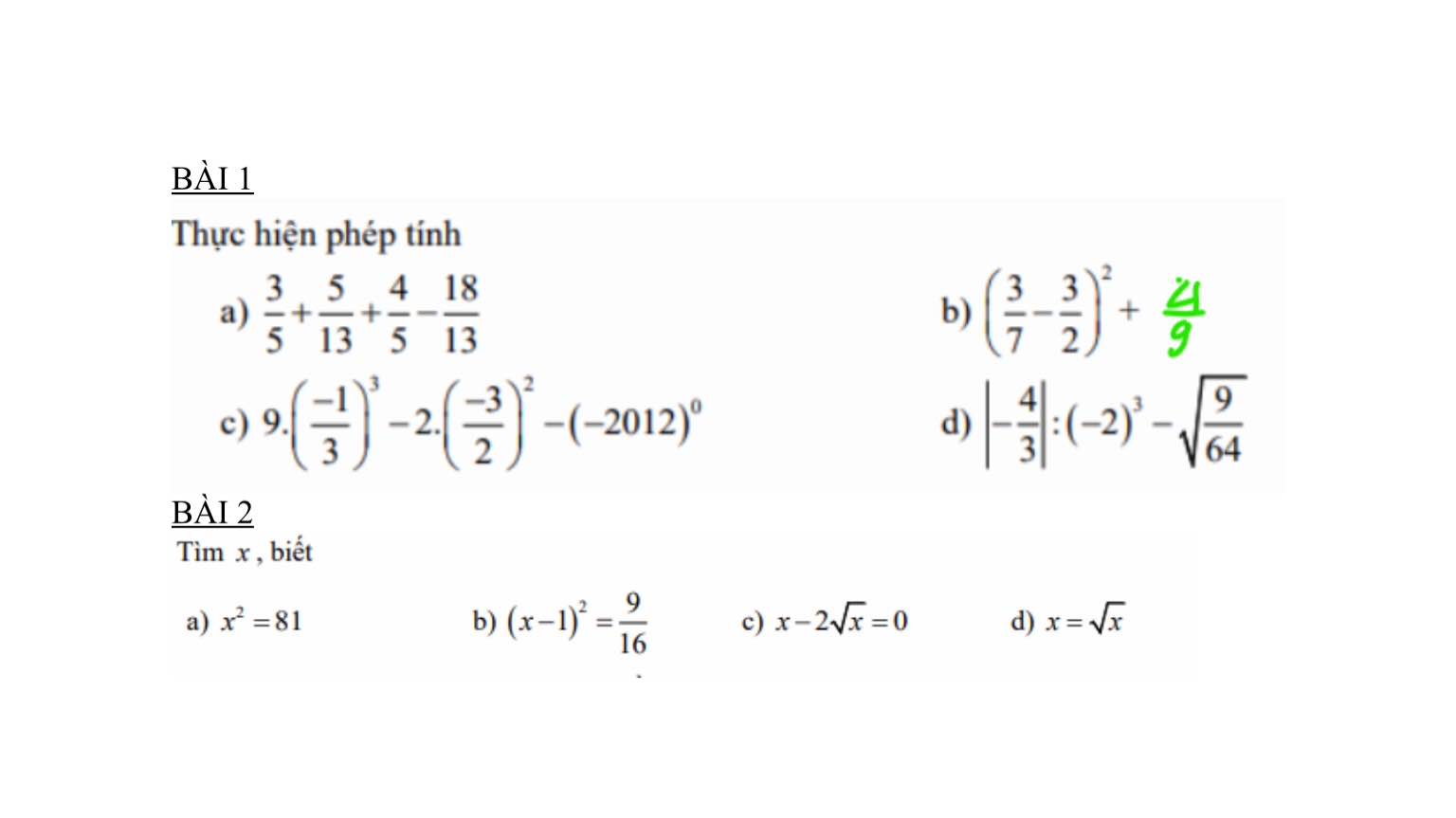 Mn lm giúp mình vs ah mình cần gấp !!!
Mn lm giúp mình vs ah mình cần gấp !!!
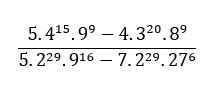
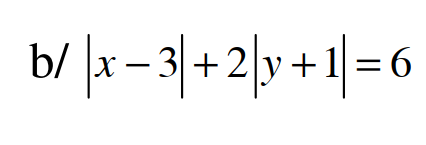



Câu 4:
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
BA=BE
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
c: Xét ΔADM vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADM}=\widehat{EDC}\)
Do đó: ΔADM=ΔEDC
Suy ra: AM=EC
Xét ΔBMC có BA/AM=BE/EC
nên AE//MC
tysm :^)