
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 2:
a: Để hai đồ thị song song thì 2m-1=m+2
hay m=3

Bài 5:
\(K=\sqrt{5x-9+6\sqrt{5x-9}+9}+\sqrt{5x-9-6\sqrt{5x-9}+9}\\ K=\sqrt{\left(\sqrt{5x-9}+3\right)^2}+\sqrt{\left(\sqrt{5x-9}-3\right)^2}\\ K=\left|\sqrt{5x-9}+3\right|+\left|3-\sqrt{5x-9}\right|\\ K\ge\left|\sqrt{5x-9}+3+3-\sqrt{5x-9}\right|=6\\ K_{min}=6\Leftrightarrow\left(\sqrt{5x-9}+3\right)\left(3-\sqrt{5x-9}\right)\ge0\\ \Leftrightarrow-3\le\sqrt{5x-9}\le3\\ \Leftrightarrow0\le5x-9\le9\\ \Leftrightarrow9\le5x\le18\\ \Leftrightarrow\dfrac{9}{5}\le x\le\dfrac{18}{5}\)

\(a,A=\dfrac{x+2\sqrt{x}+1+x-2\sqrt{x}+1-3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ A=\dfrac{2x-3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\left(\sqrt{x}-1\right)\left(2\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\\ b,A=\dfrac{2\left(\sqrt{x}+1\right)-3}{\sqrt{x}+1}=2-\dfrac{3}{\sqrt{x}+1}\in Z\\ \Leftrightarrow\sqrt{x}+1\inƯ\left(3\right)=\left\{1;3\right\}\left(\sqrt{x}+1\ge1\right)\\ \Leftrightarrow\sqrt{x}\in\left\{0;2\right\}\\ \Leftrightarrow x\in\left\{0;4\right\}\left(tm\right)\)
a) \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}+\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{3\sqrt{x}+1}{x-1}\)
\(\Rightarrow A=\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{x+2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{x+2\sqrt{x}+1+x-2\sqrt{x}+1-3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{2x-3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{\left(2x-2\sqrt{x}\right)-\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{2\sqrt{x}\left(\sqrt{x}-1\right)-\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{\left(2\sqrt{x}-1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\)

Gọi chiều rộng là x
Chiều dài là 17-x
Theo đề, ta có: \(\left(x+2\right)\left(20-x\right)=x\left(17-x\right)+45\)
\(\Leftrightarrow20x-x^2+40-2x=17x-x^2+45\)
=>18x+40=17x+45
=>x=5
Vậy: Chiều rộng là 5m
Chiều dài là 12m


\(27,B\\ 28,B\\ 29,A\\ 30,B\\ 31,D\\ 32,C\\ 33,B\\ 34,D\\ 35,A\\ 36,B\)
37. đề thiếu rồi bạn

Để M nằm ngoài đường tròn thì d>r=\(\sqrt{6}\)
Vậy loại A
Ta có \(\sqrt{6}\approx2,4495\)
Vậy loại B và D
Vậy đáp án đúng là C. d= 2,5cm







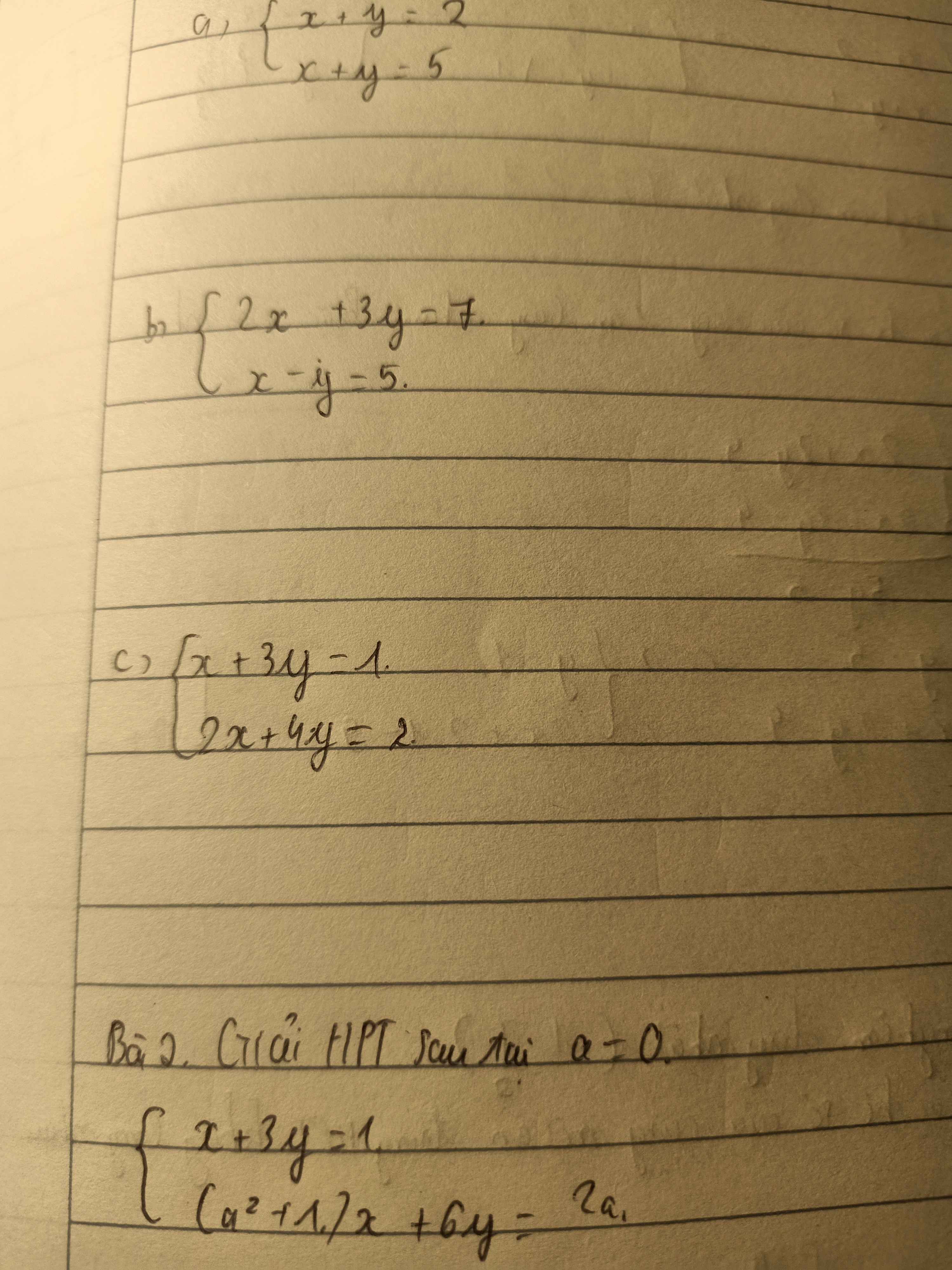 Mn giúp mình với
Mn giúp mình với
Bài 6:
a: ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\notin\left\{4;9\right\}\end{matrix}\right.\)
b: \(C=\left(1-\dfrac{x-3\sqrt{x}}{x-9}\right):\left(\dfrac{\sqrt{x}-3}{2-\sqrt{x}}+\dfrac{\sqrt{x}-2}{3+\sqrt{x}}-\dfrac{9-x}{x+\sqrt{x}-6}\right)\)
\(=\dfrac{x-9-x+3\sqrt{x}}{x-9}:\left(\dfrac{-\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}-2}{\sqrt{x}+3}+\dfrac{x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\right)\)
\(=\dfrac{3\sqrt{x}-9}{x-9}:\left(\dfrac{-\left(\sqrt{x}-3\right)}{\sqrt{x}-2}+\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}-2}{\sqrt{x}+3}\right)\)
\(=\dfrac{3\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}:\left(\dfrac{-\left(\sqrt{x}-3\right)}{\sqrt{x}-2}+\dfrac{\sqrt{x}-3}{\sqrt{x}-2}+\dfrac{\sqrt{x}-2}{\sqrt{x}+3}\right)\)
\(=\dfrac{3}{\sqrt{x}+3}:\dfrac{\sqrt{x}-2}{\sqrt{x}+3}=\dfrac{3}{\sqrt{x}-2}\)
c: C=4
=>\(\sqrt{x}-2=\dfrac{3}{4}\)
=>\(\sqrt{x}=2+\dfrac{3}{4}=\dfrac{11}{4}\)
=>\(x=\left(\dfrac{11}{4}\right)^2=\dfrac{121}{16}\left(nhận\right)\)
Câu 5:
a: ĐKXĐ: x>=0 và x<>1
b: \(B=\left(\dfrac{x+2\sqrt{x}}{x\sqrt{x}-1}-\dfrac{1}{\sqrt{x}-1}\right):\dfrac{x-1}{x+\sqrt{x}+1}\)
\(=\left(\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{1}{\sqrt{x}-1}\right)\cdot\dfrac{x+\sqrt{x}+1}{x-1}\)
\(=\dfrac{x+2\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{x+\sqrt{x}+1}{x-1}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}-1}\cdot\dfrac{1}{x-1}=\dfrac{1}{x-1}\)