TP
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DN
1
AH
Akai Haruma
Giáo viên
13 tháng 7 2023
Lời giải:
$=11(\frac{13}{161}+\frac{4}{203}-\frac{7}{413}):[5(\frac{13}{69}+\frac{4}{87}-\frac{7}{177})]$
$=11.\frac{3}{7}(\frac{13}{69}+\frac{4}{87}-\frac{7}{177}):[5(\frac{13}{69}+\frac{4}{87}-\frac{7}{177})]$
$=11.\frac{3}{7}:5=\frac{33}{35}$
LD
26 tháng 12 2021
Anh bạn à sống đẹp lên
Đấy là bài kiểm tra lên còn cái nịt nhá
TT
3
6 tháng 8 2021
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
b) Xét ΔABC có AB<AC<BC(3cm<4cm<5cm)
mà góc đối diện với cạnh AB là \(\widehat{ACB}\)
và góc đối diện với cạnh AC là \(\widehat{ABC}\)
và góc đối diện với cạnh BC là \(\widehat{BAC}\)
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
Xét ΔABC có
HB là hình chiếu của AB trên BC
HC là hình chiếu của AC trên BC
AB<AC
Do đó: HB<HC
c) Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD(gt)
Do đó: ΔCAB=ΔCAD(hai cạnh góc vuông)
Suy ra: CB=CD(hai cạnh tương ứng)
Xét ΔCBD có CB=CD(cmt)
nên ΔCBD cân tại C(Định nghĩa tam giác cân)
18 tháng 7 2021
\(a//b//c\)
\(=>\angle\left(A1\right)+\angle\left(B2\right)=180^o\)(2 góc ở vị trí trong cùng phía)
\(=>\angle\left(B2\right)=180^0-140^0=40^o\)
có \(\angle\left(B3\right)+\angle\left(B2\right)=180^o\left(ke-bu\right)\)
\(=>\angle\left(B3\right)=180^0-40^0=140^o\)
b, \(\angle\left(B2\right)+\angle\left(B1\right)=180^o\left(ke-bu\right)\)
\(=>\angle\left(B1\right)=180^o-40^o=140^o\)
\(b//c=>\angle\left(B1\right)=\angle\left(C1\right)=140^o\)(2 góc đồng vị)
\(=>\angle\left(C4\right)+\angle\left(C1\right)=180^o\left(ke-bu\right)=>\angle\left(C4\right)=180^o-140^0=40^o\)
AB
18 tháng 7 2021
Giải:
Ta có: a//b//ca//b//c
=>∠(A1)+∠(B2)=180o=>∠(A1)+∠(B2)=180o(2 góc ở vị trí trong cùng phía)
=>∠(B2)=1800−1400=40o=>∠(B2)=1800−1400=40o
có ∠(B3)+∠(B2)=180o(ke−bu)∠(B3)+∠(B2)=180o(ke−bu)
=>∠(B3)=1800−400=140o=>∠(B3)=1800−400=140o
b, ∠(B2)+∠(B1)=180o(ke−bu)∠(B2)+∠(B1)=180o(ke−bu)
=>∠(B1)=180o−40o=140o=>∠(B1)=180o−40o=140o
b//c=>∠(B1)=∠(C1)=140ob//c=>∠(B1)=∠(C1)=140o(2 góc đồng vị)
=>∠(C4)+∠(C1)=180o(ke−bu)=>∠(C4)=180o−1400=40o
HN
3
AH
Akai Haruma
Giáo viên
2 tháng 1
Câu 8:
a. Với $x,y$ là số nguyên thì $x, y-3$ cũng là số nguyên. Mà $x(y-3)=15$ nên ta có các TH:
TH1: $x=1, y-3=15\Rightarrow x=1; y=18$ (tm)
TH2: $x=-1, y-3=-15\Rightarrow x=-1; y=-12$ (tm)
TH3: $x=15; y-3=1\Rightarrow x=15; y=4$ (tm)
TH4: $x=-15; y-3=-1\Rightarrow x=-15; y=2$ (tm)
TH5: $x=3, y-3=5\Rightarrow x=3; y=8$ (tm)
TH6: $x=-3; y-3=-5\Rightarrow x=-3; y=-2$ (tm)
TH7: $x=5; y-3=3\Rightarrow x=5; y=6$ (tm)
TH8: $x=-5; y-3=-3\Rightarrow x=-5; y=0$ (tm)
AH
Akai Haruma
Giáo viên
2 tháng 1
Câu 8:
b.
$xy-2y+3(x-2)=7$
$\Rightarrow y(x-2)+3(x-2)=7$
$\Rightarrow (x-2)(y+3)=7$
Do $x,y$ nguyên nên $x-2, y+3$ nguyên. Mà tích của chúng bằng $7$ nên ta có các TH sau:
TH1: $x-2=1, y+3=7\Rightarrow x=3; y=4$ (tm)
TH2: $x-2=-1; y+3=-7\Rightarrow x=1; y=-10$ (tm)
TH3: $x-2=7, y+3=1\Rightarrow x=9; y=-2$ (tm)
TH4: $x-2=-7; y+3=-1\Rightarrow x=-5; y=-4$ (tm)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
3 tháng 8 2023
Các số được điền vào các ô theo thứ tự từ trái sang phải là:
-1; - \(\dfrac{1}{3}\); \(\dfrac{2}{3}\); \(\dfrac{4}{3}\)
TD
0
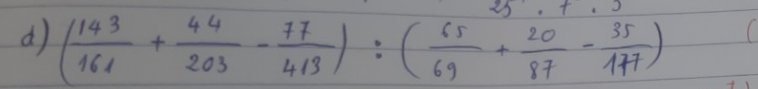
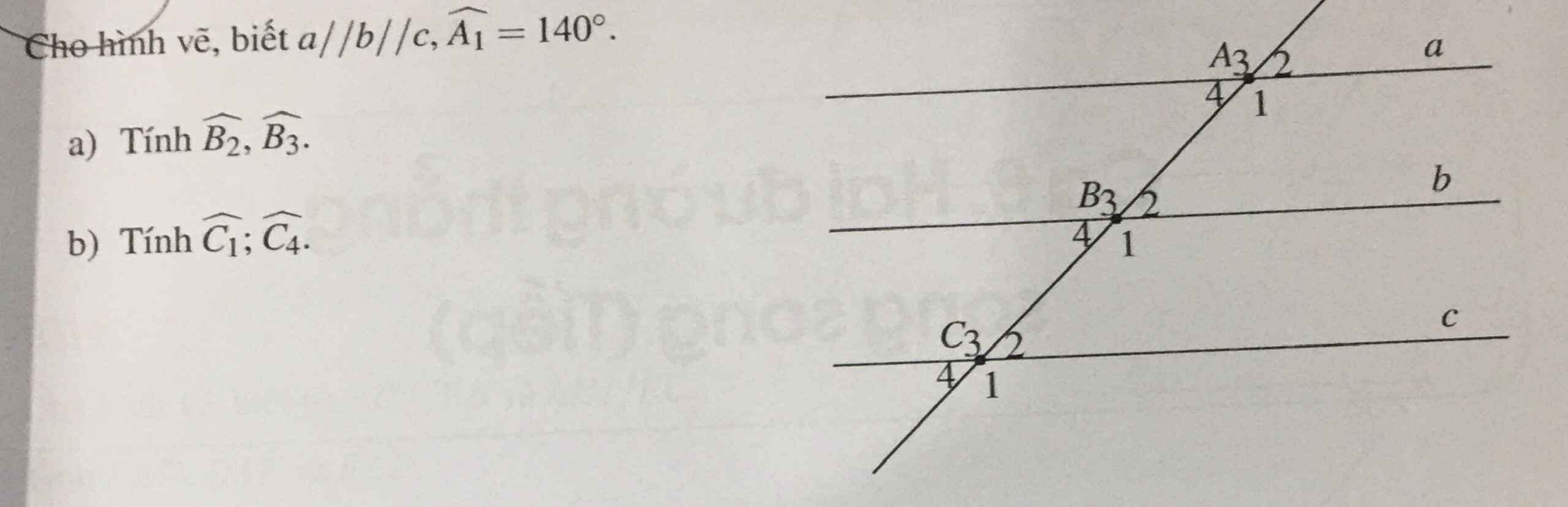
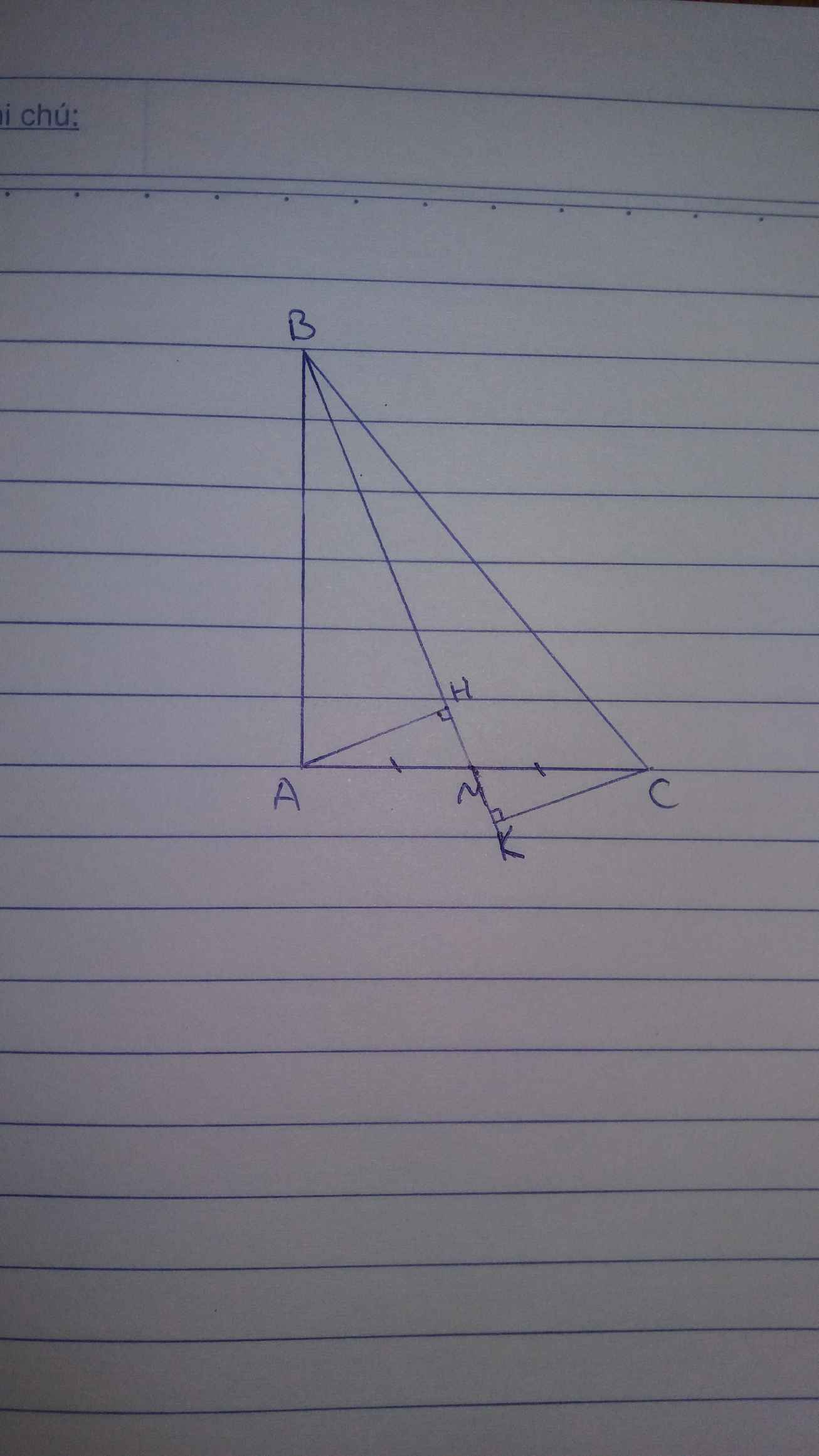
Bó tay
het cach noi loi luon