5B
Mn giúp mik với,bh mik đang cần gấp lắm 19h30 mik phải có bài r nên mn giúp mik với
6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
3 tháng 7 2023
5:
a: góc ACB=1/2*180=90 độ
Xét ΔAKH vuông tại K và ΔACB vuông tại A có
góc KAH chung
=>ΔAKH đồng dạng với ΔACB
b: Xét ΔADC và ΔBEC có
AD=BE
góc DAC=góc EBC
AC=BC
=>ΔADC=ΔBEC
=>DC=EC
=>ΔDEC cân tại C
góc CAB=45 độ
=>góc CDE=góc CAB=45 độ
=>ΔCDE vuông cân tại C
14 tháng 11 2021
\(a,\Leftrightarrow\left\{{}\begin{matrix}1-4m=-\dfrac{1}{2}\\m-2\ne3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{3}{8}\\m\ne5\end{matrix}\right.\Leftrightarrow m=\dfrac{3}{8}\\ b,\Leftrightarrow1-4m>0\Leftrightarrow m< \dfrac{1}{4}\\ c,\Leftrightarrow x=\dfrac{1}{2};y=0\Leftrightarrow\dfrac{1}{2}\left(1-4m\right)=2-m\Leftrightarrow1-4m=4-2m\\ \Leftrightarrow m=-\dfrac{3}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 10 2021
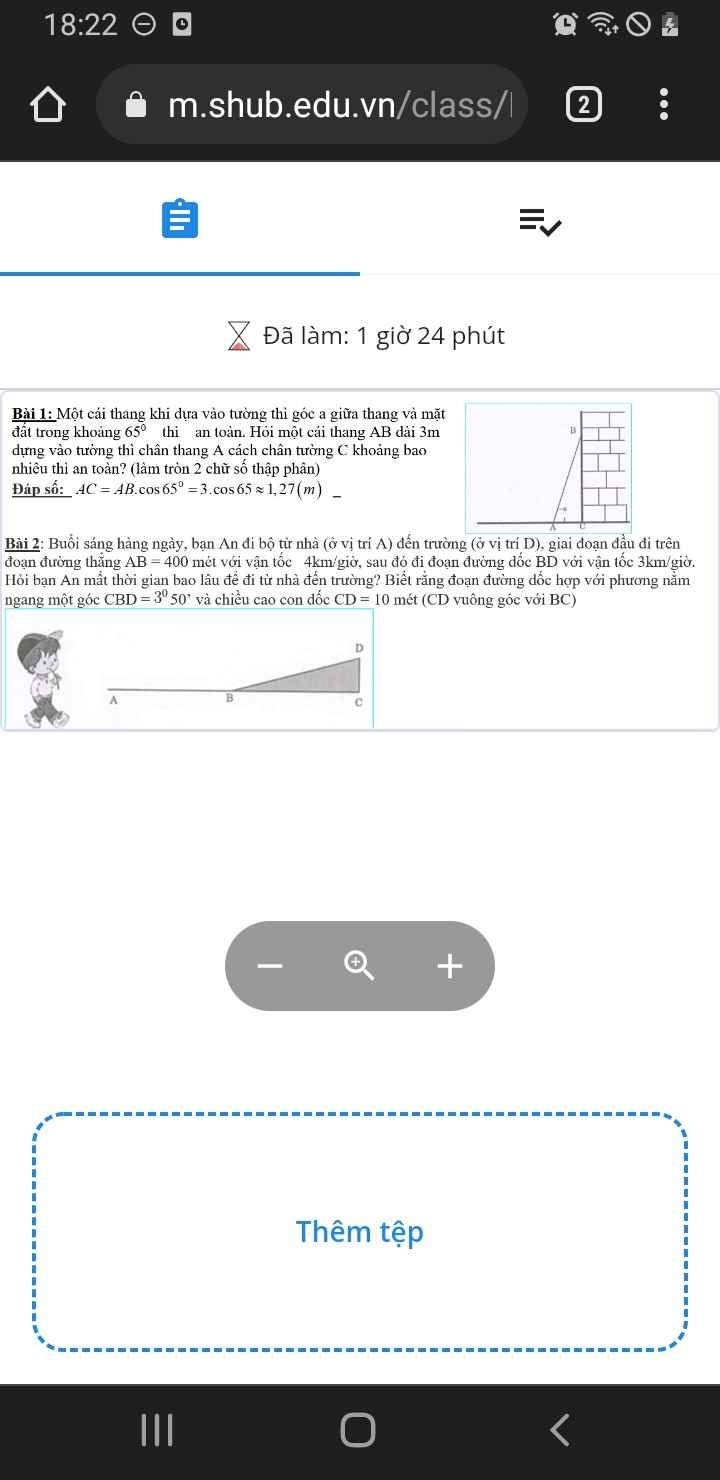
Độ dài quãng đường BD:
\(BD=\dfrac{CD}{sin\widehat{CBD}}=\dfrac{10}{sin3^050'}\approx150\left(m\right)=0,15\left(km\right)\)
Thời gian đi hết đoạn AB:
\(t_1=\dfrac{0,4}{4}=0,1\left(h\right)\)
Thời gian đi hết đoạn BD:
\(t_2=\dfrac{0,15}{3}=0,05\left(h\right)\)
Tổng thời gian:
\(t=t_1+t_2=0,15\left(h\right)=9\left(ph\right)\)
giúp mik với mn ơi mik đg cần gấp
27 tháng 10 2023
7:
a: ĐKXĐ: x>=0; x<>1
\(D=\dfrac{1}{2\sqrt{x}-2}-\dfrac{1}{2\sqrt{x}+2}+\dfrac{\sqrt{x}}{1-x}\)
\(=\dfrac{1}{2\left(\sqrt{x}-1\right)}-\dfrac{1}{2\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}+1-\sqrt{x}+1-2\sqrt{x}}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{-2\left(\sqrt{x}-1\right)}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{-1}{\sqrt{x}+1}\)
b: Khi x=4/9 thì \(D=\dfrac{-1}{\dfrac{2}{3}+1}=-1:\dfrac{5}{3}=-\dfrac{3}{5}\)
c: |D|=1/3
=>D=-1/3 hoặc D=1/3
=>\(\left[{}\begin{matrix}\dfrac{-1}{\sqrt{x}+1}=\dfrac{-1}{3}\\\dfrac{-1}{\sqrt{x}+1}=\dfrac{1}{3}\left(loại\right)\end{matrix}\right.\)
=>\(\sqrt{x}+1=3\)
=>\(\sqrt{x}=2\)
=>x=4
6:
a: \(C=\left(\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{x+9}{9-x}\right):\left(\dfrac{3\sqrt{x}+1}{x-3\sqrt{x}}-\dfrac{1}{\sqrt{x}}\right)\)
\(=\dfrac{\sqrt{x}\left(3-\sqrt{x}\right)+x+9}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}:\dfrac{3\sqrt{x}+1-\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{3\sqrt{x}-x+x+9}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}\cdot\dfrac{-\sqrt{x}\left(3-\sqrt{x}\right)}{2\sqrt{x}+4}\)
\(=\dfrac{3\left(\sqrt{x}+3\right)}{3+\sqrt{x}}\cdot\dfrac{-\sqrt{x}}{2\sqrt{x}+4}=\dfrac{-3\sqrt{x}}{2\sqrt{x}+4}\)
b: C<-1
=>C+1<0
=>\(\dfrac{-3\sqrt{x}+2\sqrt{x}+4}{2\sqrt{x}+4}< 0\)
=>\(-\sqrt{x}+4< 0\)
=>\(-\sqrt{x}< -4\)
=>\(\sqrt{x}>4\)
=>x>16
H
27 tháng 10 2023
\(C=\left(\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{x+9}{9-x}\right):\left(\dfrac{3\sqrt{x}+1}{x-3\sqrt{x}}-\dfrac{1}{\sqrt{x}}\right)\\ =\left(\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{x+9}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}\right):\left(\dfrac{3\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-3\right)}-\dfrac{1}{\sqrt{x}}\right)\\ =\left(\dfrac{\sqrt{x}\left(3-\sqrt{x}\right)}{\left(3+\sqrt{x}\right)\left(3-\sqrt{x}\right)}+\dfrac{x+9}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}\right):\left(\dfrac{3\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-3\right)}-\dfrac{\sqrt{x}-3}{\sqrt{x}\left(\sqrt{x}-3\right)}\right)\\ =\dfrac{3\sqrt{x}-x+x+9}{\left(3+\sqrt{x}\right)\left(3-\sqrt{x}\right)}:\dfrac{3\sqrt{x}+1-\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{3\sqrt{x}+9}{\left(3+\sqrt{x}\right)\left(3-\sqrt{x}\right)}\cdot\dfrac{-\sqrt{x}\left(3-\sqrt{x}\right)}{2\sqrt{x}+4}\\ =\dfrac{3\left(\sqrt{x}+3\right)}{\left(3+\sqrt{x}\right)\left(3-\sqrt{x}\right)}\cdot\dfrac{-\sqrt{x}\left(3-\sqrt{x}\right)}{2\sqrt{x}+4}\\ =\dfrac{-3\sqrt{x}}{2\sqrt{x}+4}\)
Để `C < -1` Ta có :
\(\dfrac{-3}{2\sqrt{x}+4}< -1\\ \Leftrightarrow\dfrac{-3}{2\sqrt{x}+4}+1< 0\\ \Leftrightarrow\dfrac{-3}{2\sqrt{x}+4}+\dfrac{2\sqrt{x}+4}{2\sqrt{x}+4}< 0\\ \Leftrightarrow-3+2\sqrt{x}+4< 0\\ \Leftrightarrow2\sqrt{x}+1< 0\\ \Leftrightarrow2\sqrt{x}< -1\\ \Leftrightarrow\sqrt{x}< -\dfrac{1}{2}\\ \Leftrightarrow x< \dfrac{1}{4}\)
lên mạng mà tìm