
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 4:
a) Thay x=49 vào B ta có:
\(B=\dfrac{1-\sqrt{49}}{1+\sqrt{49}}=-\dfrac{3}{4}\)
b) \(A=\left(\dfrac{15-\sqrt{x}}{x-25}+\dfrac{2}{\sqrt{x}+5}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-5}\)
\(A=\left[\dfrac{15-\sqrt{x}}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}+\dfrac{2\left(\sqrt{x}-5\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\right]\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+1}\)
\(A=\dfrac{15-\sqrt{x}+2\sqrt{x}-10}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+1}\)
\(A=\dfrac{\sqrt{x}+5}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+1}\)
\(A=\dfrac{1}{\sqrt{x}-5}\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+1}\)
\(A=\dfrac{1}{\sqrt{x}+1}\)
c) Ta có:
\(M=A-B=\dfrac{1}{\sqrt{x}+1}-\dfrac{1-\sqrt{x}}{\sqrt{x}+1}\)
\(M=\dfrac{1-1+\sqrt{x}}{\sqrt{x}+1}\)
\(M=\dfrac{\sqrt{x}}{\sqrt{x}+1}\)
\(M=\dfrac{\sqrt{x}+1-1}{\sqrt{x}+1}=\dfrac{\sqrt{x}+1}{\sqrt{x}+1}-\dfrac{1}{\sqrt{x}+1}=1-\dfrac{1}{\sqrt{x}+1}\)
Mà M nguyên khi:
\(1\) ⋮ \(\sqrt{x}+1\)
\(\Rightarrow\sqrt{x}+1\in\left\{1;-1\right\}\)
Mà: \(\sqrt{x}+1\ge1\)
\(\Rightarrow\sqrt{x}+1=1\)
\(\Rightarrow\sqrt{x}=0\)
\(\Rightarrow x=0\left(tm\right)\)
Vậy M nguyên khi x=0


Bài 6:
a: Ta có: \(E=\dfrac{1}{\sqrt{x}+1}:\left(\dfrac{1}{\sqrt{x}}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right)\)
\(=\dfrac{1}{\sqrt{x}+1}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{x+\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)

Bài 4:
b: Xét ΔABK vuông tại A có AD là đường cao ứng với cạnh huyền BK
nên \(BD\cdot BK=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)

1.
d, ĐK: \(x\ge-5\)
\(x-2-4\sqrt{x+5}=-10\)
\(\Leftrightarrow x+5-4\sqrt{x+5}+3=0\)
\(\Leftrightarrow\left(\sqrt{x+5}-1\right)\left(\sqrt{x+5}-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x+5}=1\\\sqrt{x+5}=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+5=1\\x+5=9\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=4\end{matrix}\right.\)
\(\Leftrightarrow x=\pm4\left(tm\right)\)
2.
ĐK: \(x\in R\)
\(\sqrt{x^2+2x+1}+\sqrt{x^2-4x+4}=3\)
\(\Leftrightarrow\sqrt{\left(x+1\right)^2}+\sqrt{\left(x-2\right)^2}=3\)
\(\Leftrightarrow\left|x+1\right|+\left|x-2\right|=3\)
Áp dụng BĐT \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\).
\(\left|x+1\right|+\left|x-2\right|=\left|x+1\right|+\left|2-x\right|\ge\left|x+1+2-x\right|=3\)
Đẳng thức xảy ra khi:
\(\left(x+1\right)\left(2-x\right)\ge0\)
\(\Leftrightarrow-1\le x\le2\)

Bài 1:
c: Vì a+b+c=0 nên phương trình có hai nghiệm phân biệt là
x1=1; \(x2=\dfrac{c}{a}=\dfrac{3\sqrt{2}+1}{1-\sqrt{2}}\)

`D=(sqrt{3}.sqrt{5-2sqrt6})/(sqrt3-sqrt2)-1/(2-sqrt3)`
`=(sqrt3*sqrt{3-2sqrt{3}.sqrt2+2})/(sqrt3-sqrt2)-(2+sqrt3)/(4-3)`
`=(sqrt3.sqrt{(sqrt3-sqrt2)^2})/(sqrt3-sqrt2)-2-sqrt3`
`=sqrt3-2-sqrt3=-2`

b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HM là đường cao ứng với cạnh huyền AB, ta được:
\(AM\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC, ta được:
\(AN\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)


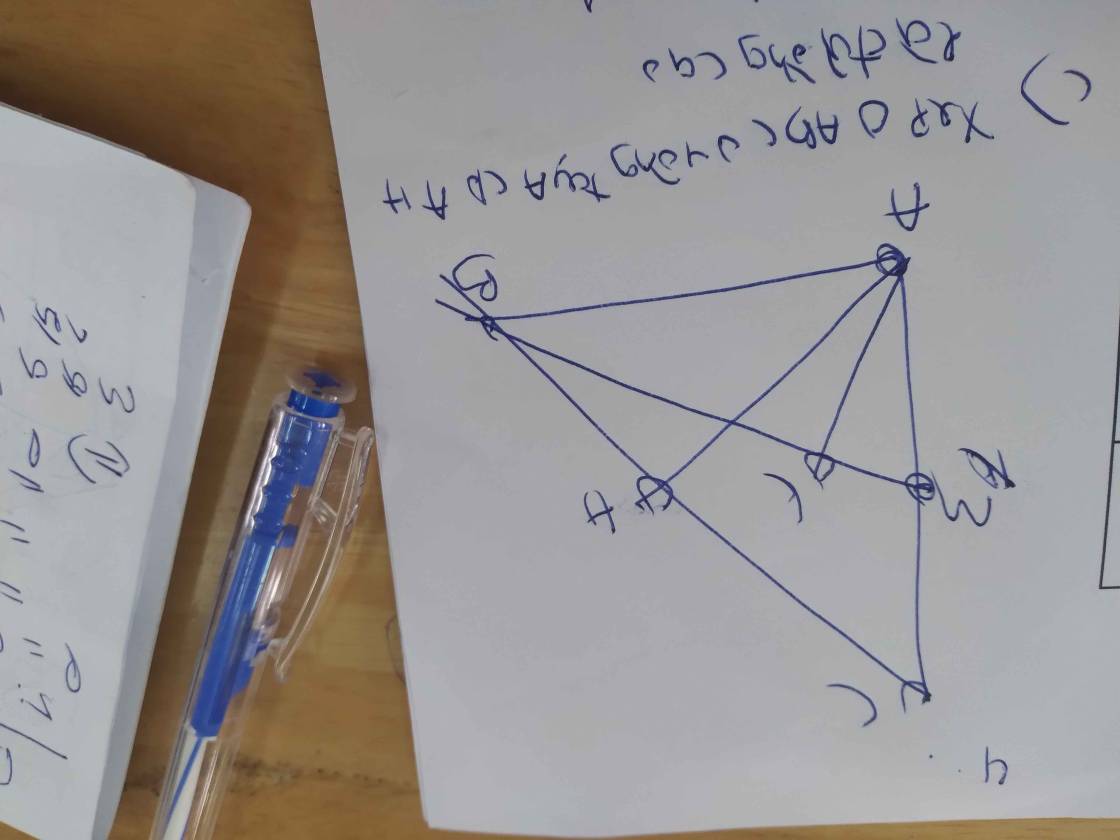


 mn giúp e câu C của bài 4 và 5 với ạ,em cảm ơn
mn giúp e câu C của bài 4 và 5 với ạ,em cảm ơn
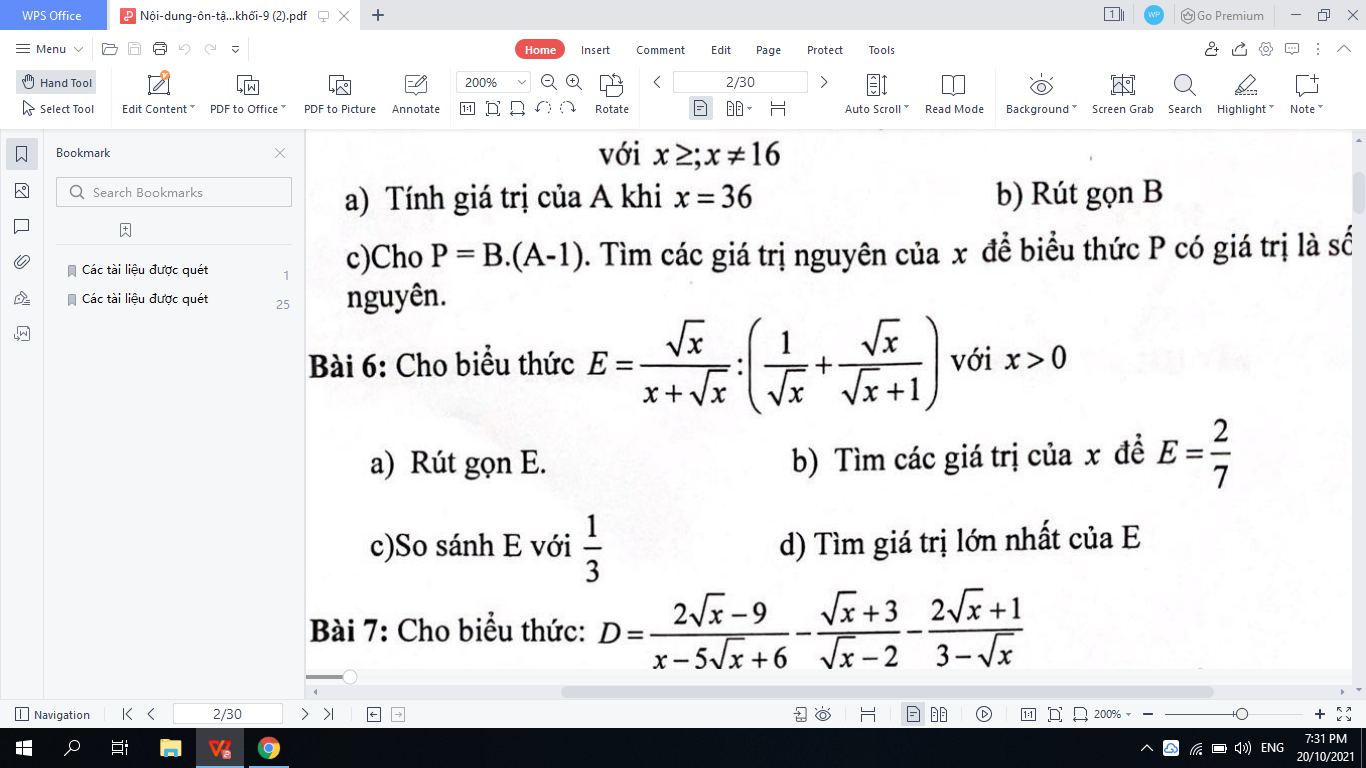
 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn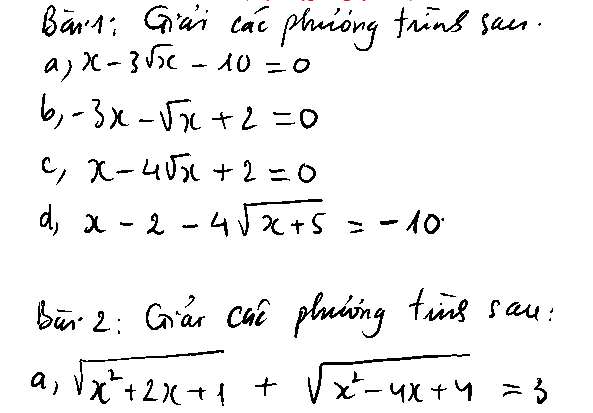
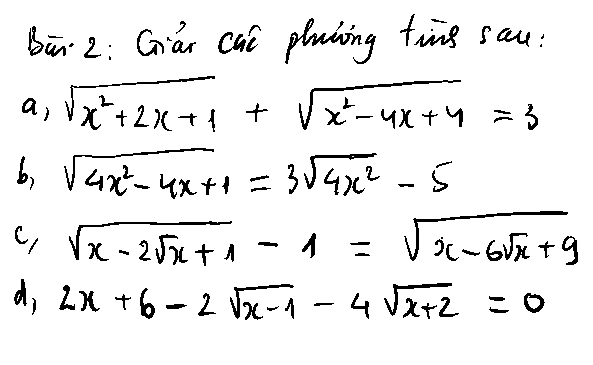


 Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Bạn ơi câu c bài 1 mà