
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


khi bài toán bắt ta chứng minh một hình gì đó mà thiếu một ta hay một đường thẳng...

2:
a: A=căn 3-1-2-căn 3=-3
b: =căn 3+căn 2-căn 3+căn 2=2*căn 2
d: =(căn 7/2+căn 5/2)*(căn 7-căn 5)=2/2=1
e: =3-căn 5+2căn 5+2-căn 5+2
=7

ĐKXĐ: \(\left\{{}\begin{matrix}2x+5>=0\\4-2x>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x>=-5\\2x< =4\end{matrix}\right.\Leftrightarrow-\dfrac{5}{2}< =x< =2\)
\(x^2+\sqrt{2x+5}+\sqrt{4-2x}=4x-1\)
=>\(x^2-4+\sqrt{2x+5}-3+\sqrt{4-2x}=4x-1-7\)
=>\(\left(x-2\right)\left(x+2\right)+\dfrac{2x+5-9}{\sqrt{2x+5}+3}+\sqrt{4-2x}=4x-8\)
=>\(\left(x-2\right)\left[\left(x+2\right)+\dfrac{2}{\sqrt{2x+5}+3}-4\right]+\sqrt{4-2x}=0\)
=>\(-\left(2-x\right)\left[\left(x-2\right)+\dfrac{2}{\sqrt{2x+5}+3}\right]+\sqrt{2\left(2-x\right)}=0\)
=>\(\sqrt{2-x}\left[-\sqrt{2-x}\left(x-2+\dfrac{2}{\sqrt{2x+5}+3}\right)+\sqrt{2}\right]=0\)
=>\(\sqrt{2-x}=0\)
=>x=2(nhận)

3:
ĐKXĐ: x>=0; x<>1
a: \(P=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\)
\(=\left(\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}\right)\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)^2}\cdot\dfrac{2}{x+\sqrt{x}+1}=\dfrac{2}{x+\sqrt{x}+1}\)
b: \(x+\sqrt{x}+1=\sqrt{x}\left(\sqrt{x}+1\right)+1>=0+1=1\)
=>\(x+\sqrt{x}+1>0\forall x\) thỏa mãn ĐKXĐ
mà 2>0
nên \(P=\dfrac{2}{x+\sqrt{x}+1}>0\forall x\) thỏa mãn ĐKXĐ

Giả sử x lớn hơn y
Thấy x2 + 8y lớn hơn x2 và nhỏ hơn x2 + 8x nhỏ hơn (x + 4)2 suy ra nó nằm giữa 2 cái bình phương vừa nêu. Áp dụn chẵn lẻ loại 2 th suy ra 2y = x + 1 thay vào y2 + 8x là ra thôi. Thầy mình ra bài này thấy dễ quá định lên mạng chép mà mấy thằng thông minh không rảnh mà lên mạng. Với cả thay vào y2 + 8x kẹp tiếp bạn nhé rồi xét TH. Xong 😅


9.
a, \(x^4-x^3-14x^2+x+1=0\)
\(< =>x^4+3x^3-x^2-4x^3-12x^2+4x-x^2-3x+1=0\)
\(< =>x^2\left(x^2+3x-1\right)-4x\left(x^2+3x-1\right)-\left(x^2+3x-1\right)=0\)
\(< =>\left(x^2-4x-1\right)\left(x^2+3x-1\right)=0\)
\(=>\left[{}\begin{matrix}x^2-4x-1=0\left(1\right)\\x^2+3x-1=0\left(2\right)\end{matrix}\right.\)
giải pt(1) \(=>x^2-4x+4-5=0< =>\left(x-2\right)^2-\sqrt{5}^2=0\)
\(=>\left(x-2-\sqrt{5}\right)\left(x-2+\sqrt{5}\right)=0\)
\(=>\left[{}\begin{matrix}x=2+\sqrt{5}\\x=2-\sqrt{5}\end{matrix}\right.\)
giải pt(2) \(\)\(=>x^2+3x-1=0< =>x^2+2.\dfrac{3}{2}x+\dfrac{9}{4}-\dfrac{13}{4}=0\)
\(< =>\left(x+\dfrac{3}{2}\right)^2-\left(\dfrac{\sqrt{13}}{2}\right)^2=0\)
\(=>\left(x+\dfrac{3}{2}+\dfrac{\sqrt{13}}{2}\right)\left(x+\dfrac{3}{2}-\dfrac{\sqrt{13}}{2}\right)=0\)
tương tự cái pt(1) ra nghiệm rồi kết luận
b, đặt \(\sqrt{x^2+1}=a\left(a\ge1\right)=>x^2+1=a^2\)
\(=>x^4=\left(a^2-1\right)^2\)
\(=>pt\) \(\left(a^2-1\right)^2+a^2.a-1=0\)
\(=>a^4-2a^2+1+a^3-1=0\)
\(< =>a^4-2a^2+a^3=0< =>a^2\left(a+2\right)\left(a-1\right)=0\)
\(->\left[{}\begin{matrix}a=0\left(ktm\right)\\a=-2\left(ktm\right)\\a=1\left(tm\right)\end{matrix}\right.\)rồi thế a vào \(\sqrt{x^2+1}\)
\(=>x=0\)

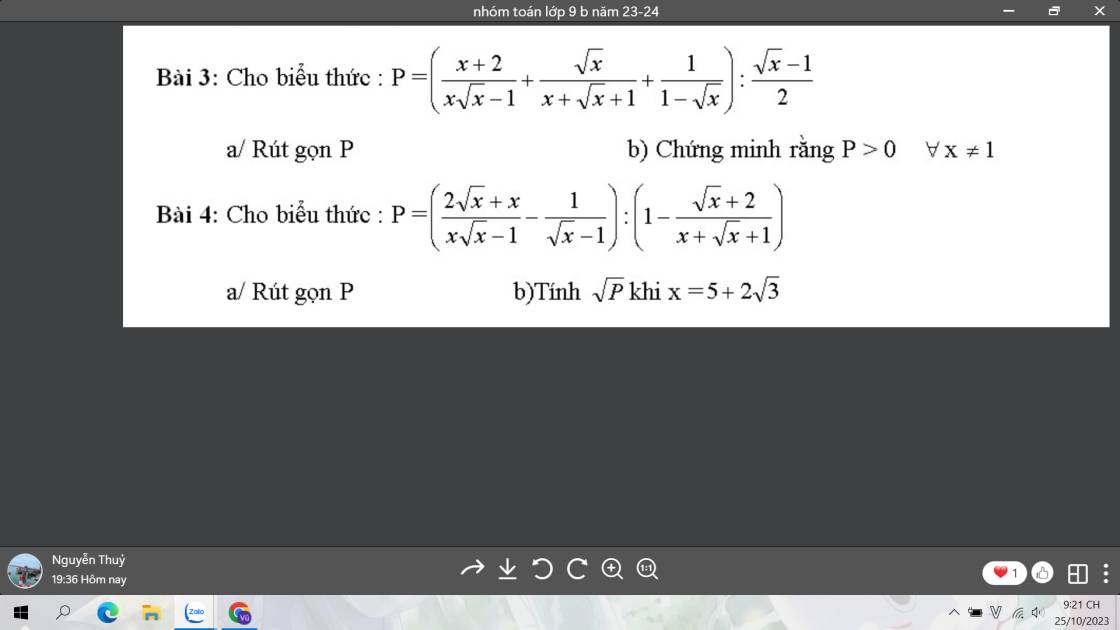 giải giúp mik bài 3 nha mn <3
giải giúp mik bài 3 nha mn <3





Bài 2:
Ta có
OA=OC => tg OAC cân tại O \(\Rightarrow\widehat{OCA}=\widehat{OAC}\) (1)
\(\Rightarrow\widehat{AOC}=180^o-\left(\widehat{OCA}+\widehat{OAC}\right)\) (2)
O'A=O'B => tg O'AB cân tại O' \(\Rightarrow\widehat{O'AB}=\widehat{O'BA}\) (3)
\(\Rightarrow\widehat{AO'B}=180^o-\left(\widehat{O'AB}+\widehat{O'BA}\right)\) (4)
\(\widehat{OAC}=\widehat{O'AB}\) (5)
Từ (1) (2) (3) (4) (5) \(\Rightarrow\widehat{AOC}=\widehat{AO'B}\)
Xét đường tròn (O)
\(sđ\widehat{AOC}=sđ\)cung AC (góc ở tâm)
Xét đường tròn (O')
\(sđ\widehat{AO'B}=sđ\) cung AB (góc ở tâm)
=> sđ cung AC = sđ cung AB
\(\Rightarrow sđ\widehat{ACy}=\frac{1}{2}sđ\)cung AC \(=\frac{1}{2}sđ\) cung AB \(=sđ\widehat{ABx}\) (góc nội tiếp đường tròn)
=> Bx//Cy (Hai đường thẳng bị cắt bởi đường thẳng thứ 3 tạo thành 2 góc sole trong = nhau thì // với nhau) (đpcm)