Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a.\(y'=x\left(\sqrt{x^2-2x}\right)'+\sqrt{x^2-2x}=\dfrac{x}{2\sqrt{x^2-2x}}2\left(x-1\right)+\sqrt{x^2-2x}=\dfrac{x\left(x-1\right)}{\sqrt{x^2-2x}}+\sqrt{x^2-2x}\)
\(=\dfrac{x^2-x+x^2-2x}{2\sqrt{x^2-2x}}=\dfrac{2x^2-3x}{2\sqrt{x^2-2x}}\)
b. \(y=3sin2x+cos3x\Rightarrow y'=6cos2x-3sin3x\)
bài này dễ thôi bạn
thay x= x+ k6pi vào hàm số y=f(x)= sin\(\frac{x}{3}\) ta dc
sin\(\frac{x+k6pi}{3}\) =sin\(\frac{x}{3}+k2pi\) ( vì k2pi "số chẵn lần của π" nên có thể bỏ được)
suy ra sin\(\frac{x}{3}\) =sin\(\frac{x}{3}\) =f(x) ( dpcm)
a) Không thể tìm được giá trị chính xác cho mốt của mẫu số liệu gốc về thời gian xem ti vi của học sinh
b) Tần số lớn nhất là 16 nên nhóm chứa mốt là [5;10)
Ta có \(j = 2,\;{a_2} = 5,\;{m_2} = 16,\;{m_1} = 8;\;{m_3} = 4,\;h = 5.\) Do đó,
\({M_0} = 5 + \frac{{16 - 8}}{{\left( {16 - 8} \right) + \left( {16 - 4} \right)}} \times 5 = 7\).
- Ta có:
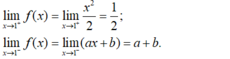
- Hàm số đã cho có đạo hàm tại x = 1 nên hàm số liên tục tại x = 1.
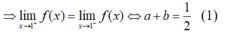
- Hàm số có đạo hàm tại x = 1 nên giới hạn 2 bên của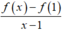 
bằng nhau, ta có:
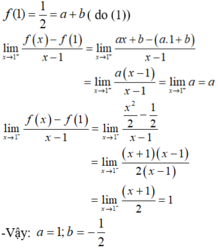
Chọn A.
Cảm ơn nhé!
Đăng ảnh trực tiếp thì không được, nhưng bạn đăng ngay dưới bình luận như vầy thì thoải mái (trong khung bình luận có chỗ tải ảnh lên cạnh biểu tượng emo mặt cười đó)