Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử Minh và Nam đi theo đường MI'N . Gọi điểm N' là điểm đối xứng N qua bãi sông.
Ta có : MI'N = MI' + I'N = MI' + I'N' = MI'N'
Để MI'N ngắn nhất thì ba điểm M;I';N' thẳng hàng. Lúc đó I = I'
=> NP = NK - PK = NK - NH = 450 (m)
\(MP=\sqrt{MN^2-NP^2}=600\left(m\right)\)
N'P = N'K + KP = 750 (m)
\(MN'=\sqrt{MP^2+N'P^2}=150\sqrt{41}\left(m\right)\)
Thời gian ngắn nhất là :
\(t=\frac{MN'}{V}=\frac{150\sqrt{41}}{2}=75\sqrt{41}=480\left(s\right)=8\left(phút\right)\)
Giả sử Minh và Nam đi theo đường MI'N . Gọi điểm N' là điểm đối xứng N qua bãi sông.
Ta có : MI'N = MI' + I'N = MI' + I'N' = MI'N'
Để MI'N ngắn nhất thì ba điểm M;I';N' thẳng hàng. Lúc đó I = I'
=> NP = NK - PK = NK - NH = 450 (m)
MP=√MN2−NP2=600(m)
N'P = N'K + KP = 750 (m)
MN'=√MP2+N'P2=150√41(m)
Thời gian ngắn nhất là :
t=MN'V =150√412 =75√41=480(s)=8(phút)

Vx là vận tốc xuôi,Vcn là vậ tốc ca nô
Vn vận tốc nước
Vng là vận tốc ngược:
=> Vx=S/tx=60/2=30
Vng=S/tng=60/3=20
mà Vx=Vcn+Vn
Vng=Vcn-Vn
=> Vcn=Vx+Vng/2=25
Vn=30-25=5

Gọi vận tốc thực của ca nô là: x (km/giờ) (ĐK: x > 0)
Thời gian đi xuôi dòng là: 9/(2 + x) (giờ)
Thời gian đi ngược dòng là: 8/(2 - x) (giờ)
=> Ta có PT:
\(\frac{8}{\left(2-x\right)}-\frac{9}{\left(2+x\right)}=\frac{1}{4}\)
\(\Leftrightarrow\orbr{\begin{cases}x=10\left(\text{TM}\right)\\x=-14\left(\text{loai}\right)\end{cases}}\)
Ta có: 15 phút =\(\frac{1}{4}\)giờ
Gọi vân tốc cano khi nước đứng yên là x,x>0 và tính bằng km/h
Đến đây, có 4 đại lượng biểu diễn là:
-Vận tốc cano xuôi dòng
-Vận tốc cano đi ngược dòng
-Thời gian cano đi xuôi dòng
-Thời gian cano đi ngược dòng
Các đại lượng này được thể hiện trong bảng sau
| Xuôi dòng | Ngược dòng | Chênh lệch | |
| Vận tốc | x+2 | x-2 | |
| Thời gian | \(\frac{9}{x+2}\) | \(\frac{8}{x-2}\) | \(\frac{8}{x-2}-\frac{9}{x+2}\) |
Nhìn vào bảng, ta dễ dàng lập phương trình:
\(\frac{8}{x-2}-\frac{9}{x+2}=\frac{1}{4}\)ĐK: \(x\ne\pm2\)
Mẫu chung là: 4(x-2)(x+2)
Quy đồng và khử mẫu, ta đưa về phương trình
x2+4x-140=0
<=> (x-10)(x+14)=0
<=> x1=10; x2=-14
Giá trị x2=-14 (loại) vì x>0
Vậy vận tốc thực của cano là 10km/h
*Trình bày bài bạn không cần đưa bảng vào nhé*

15 phút = (1/4)giờ
Gọi vận tốc của ca nô khi nước đứng yên là x (km/h). Điều kiện x > 2
Vận tốc ca nô khi xuôi dòng là x + 2 (km/h)
Vận tốc ca nô khi ngược dòng là x – 2 (km/h)
Thời gian ca nô khi xuôi dòng là:
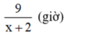
Thời gian ca nô khi ngược dòng là:
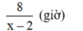
Ta có phương trình:
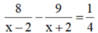
Quy đồng mẫu hai vế:
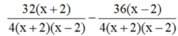
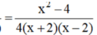
Suy ra:
32x + 64 - 36x + 72 = x2 - 4
⇔ -4x + 136 = x2 - 4
⇔ x2 + 4x - 140 = 0
⇔ (x2 + 4x + 4) - 144 = 0
⇔ (x + 2)2 - 122 = 0
⇔ (x + 14)(x - 10) = 0
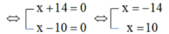
Giá trị x = -14 không thỏa mãn điều kiện
Giá trị x = 10 thỏa mãn điều kiện
Vậy vận tốc của ca nô khi nước yên lặng là 10km/h

Gọi vận tốc thực của tàu khi nước yên lặng là x km/h (x>o)
vận tốc của thuyền lúc đi là x-4 km/h
vận tốc của thuyền lúc về là x+4 km/h
thời gian thuyền di đến bến bên kia la 80/(x-4) h
thời gian thuyền di được khi quay về la 80/(x+4) h
vì thời gian cả di lẩn về là 8h20' (hay 25/3 h) nên ta có pt:
80/(x+4) + 80/(x-4) = 25/3
<=> 240x-960+240x+960=25x^2-400
<=> 25x^2-480x-400=0
dental' = (-240)^2 +25*400= 67600 (>0) căn dental'= 240
vậy pt có hai nghiệm
x1= (240-260)/25= -0,8 (loại)
x2=(240+260)/25=20 (nhận)
vậy vận tốc của tàu khi nước yên lặng là 20 km/h
Chúc bạn học tốt!!
Gọi Vriêng(canô) là x(km/h).Điều kiện x>4
Vận tốc xuôi: x+ 4
vận tốc ngược x-4
=> Thời gian xuôi: 80/x+4
Thời gian ngược 72/x-4
Ta có pt: 72/(x-4)-80/(x+4)=0,25
<=>72(x+4)-80(x-4)=0,25(x+4)(x-4)
<=>-8x+608=0,25(x²-16)
<=>-32x+2432=x²-16
<=>x²-36x+68x-2448=0
<=>(x-36)(x+68)=0
Giải pt ta được x= 36 ( thỏa mãn)
vậy vận tốc riêng của ca nô là 36 km/h