K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TG
0
18 tháng 10 2021
bn tìm ảnh của một điểm bất kì nằm trên đường thẳng qua phép tịnh tiến
vd : bn ra là m phẩy thông qua x và y r thay m phẩy vào phương trình cũ là ra
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 4 2022
5.
\(y=\dfrac{2x-1}{1-x}\Rightarrow y'=\dfrac{\left(2x-1\right)'\left(1-x\right)-\left(1-x\right)'\left(2x-1\right)}{\left(1-x\right)^2}\)
\(=\dfrac{2\left(1-x\right)+\left(2x-1\right)}{\left(1-x\right)^2}=\dfrac{1}{\left(1-x\right)^2}=\dfrac{1}{\left(x-1\right)^2}\)
9.
\(\lim\limits\dfrac{2n^2+4}{3-n^2}=\lim\dfrac{2+\dfrac{4}{n^2}}{\dfrac{3}{n^2}-1}=\dfrac{2+0}{0-1}=-2\)
PA
1
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 6 2021
\(\Leftrightarrow sin\left(2x+\dfrac{\pi}{3}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+\dfrac{\pi}{3}=\dfrac{\pi}{6}+k2\pi\\2x+\dfrac{\pi}{3}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{12}+k\pi\\x=\dfrac{\pi}{4}+k\pi\end{matrix}\right.\)
Nghiệm dương nhỏ nhất là \(x=\dfrac{\pi}{4}\approx0.79\)
Đáp án C
TA
15 tháng 6 2021
Có: `y=a sinx +b cosx`
`=> -\sqrt(a^2+b^2) <= y <= \sqrt(a^2+b^2)`
TA
15 tháng 6 2021
- Nhớ sương sương vậy thôi chứ câu từ đầy đủ thế nào thì bạn tự tra mạng nkaaaa.
TA
6 tháng 8 2021
b) `sin^2 3x=1`
`<=> (1-cos6x)/2=1`
`<=> 1-cos6x=2`
`<=> cos6x=-1`
`<=> 6x=π +k2π`
`<=>x=π/6 +k π/3 ( k \in ZZ)`
c) `tan^2 2x=3`
`<=> (1-cos4x)/(1+cos4x)=3`
`<=> 1-cos4x=3+3cos4x`
`<=>cos4x = -1/2`
`<=>4x= \pm (2π)/3 +k2π`
`<=>x = \pm π/6 + k π/2 (k \in ZZ)`
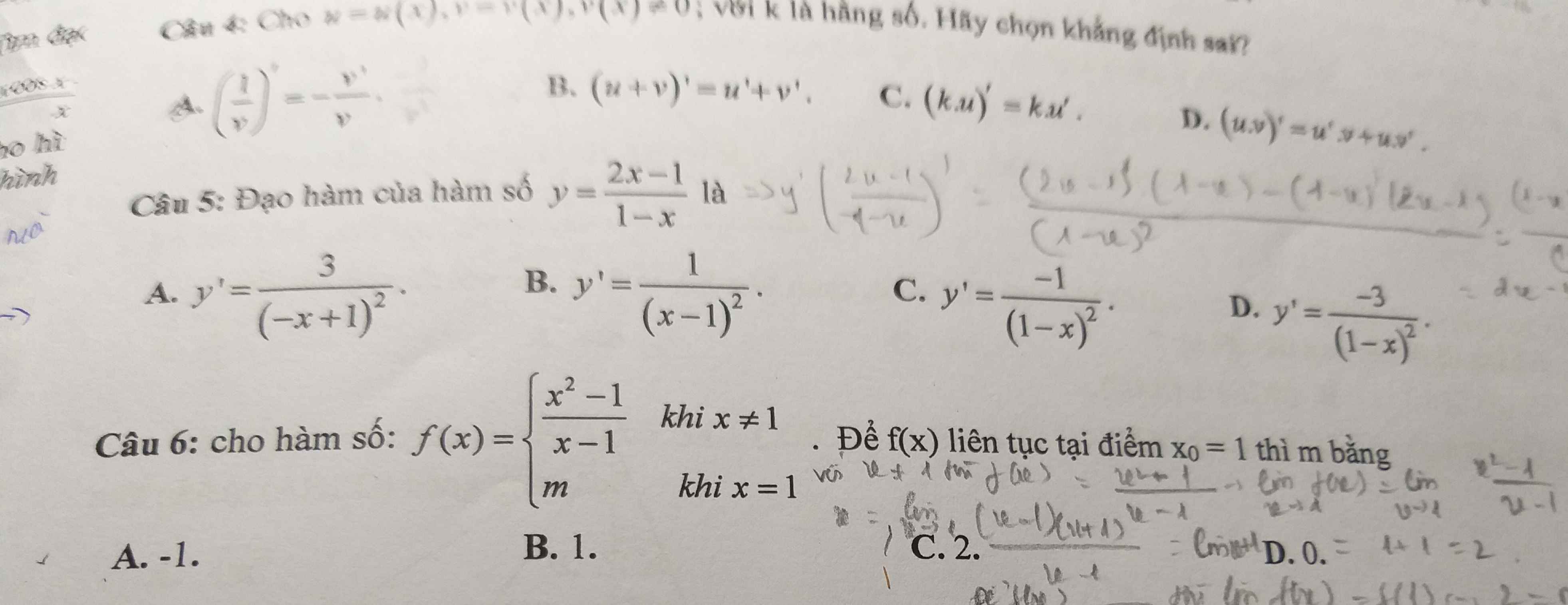
Câu 2:
SHTQ là: \(C^k_{12}\cdot\left(2x\right)^{12-k}\cdot\left(-\dfrac{1}{x^2}\right)^k=C^k_{12}\cdot\left(-1\right)^k\cdot2^{12-k}\cdot x^{12-3k}\)
Số hạng ko chứa x tương ứng với 12-3k=0
=>k=4
=>Số hạng ko chứa x là \(C^4_{12}\cdot\left(-1\right)^4\cdot2^{12-4}=126720\)