Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng hệ thức giữa cạnh và góc, ta có:
\(HB=AH.cotgB;HC=AH.cotgC\)
\(\Rightarrow AH=\frac{HB+HC}{cotgB+cotgC}=\frac{20}{cotg40^o+cotg30^o}\approx6,84\left(cm\right)\)
Lại áp dụng hệ thức giữa cạnh và góc, ta có:
\(AB=\frac{AH}{sinB}\approx\frac{6,84}{sin40^o}\approx10,64\left(cm\right)\)
\(AC=\frac{AH}{sinC}\approx\frac{6,84}{sin30^o}=13,68\left(cm\right)\)

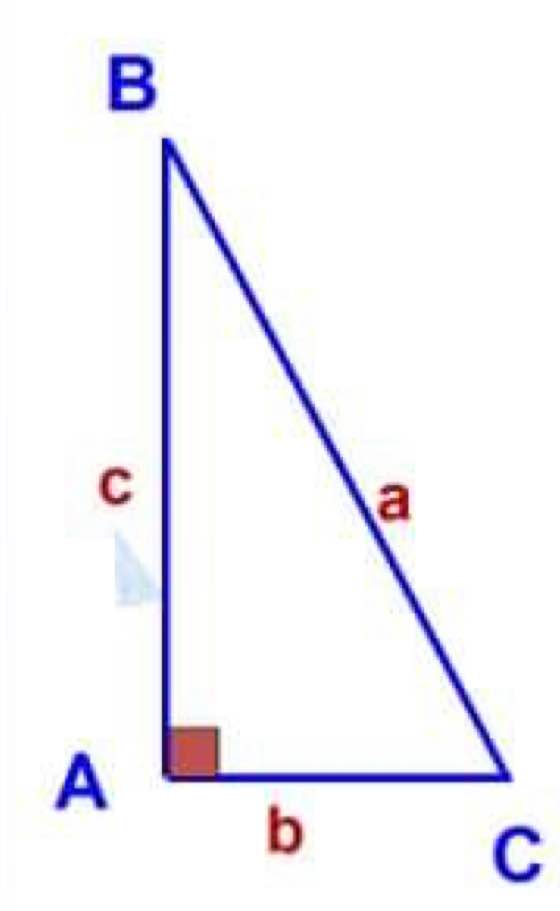
a: \(\sin\widehat{B}=\cos\widehat{C}=\dfrac{AC}{BC}\)
\(\cos\widehat{B}=\sin\widehat{C}=\dfrac{AB}{BC}\)
\(\tan\widehat{B}=\cot\widehat{C}=\dfrac{AC}{AB}\)
\(\cot\widehat{B}=\tan\widehat{C}=\dfrac{AB}{AC}\)

Định lí PYTAGO cho tam giác ABC vuông tại A: \(BC^2=AB^2+AC^2=2AB^2\Rightarrow BC=AB\sqrt{2}\)
Xét tam giác ABC vuông tại A: \(sinB=\frac{AC}{BC}=\frac{AB}{AB\sqrt{2}}=\frac{\sqrt{2}}{2}\)\(cosB=\frac{AB}{BC}=\frac{AB}{AB\sqrt{2}}=\frac{\sqrt{2}}{2}\)
\(tanB=\frac{AC}{AB}=\frac{AB}{AB}=1\), \(cotB=\frac{AB}{AC}=\frac{AB}{AB}=1\)
Vì tam giác ABC vuông cân tại A-->B=450
Vậy \(sin45^0=cos45^0\frac{\sqrt{2}}{2},tan45^0=cot45^0=1\)
,