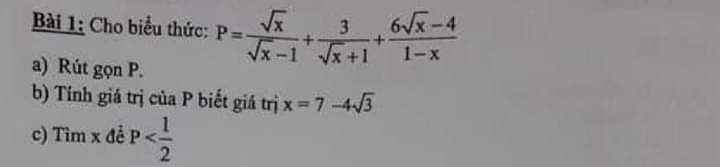Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt{4x-20}\)- 3\(\sqrt{\dfrac{x-5}{9}}\)=2
= \(\sqrt{4x-4.5}\)-3\(\sqrt{\dfrac{x-5}{9}}\)=2
= 2.2\(\sqrt{x-5}\)-3.9\(\sqrt{x-5}\)=2
= -23\(\sqrt{x-5}\)=2
= -23.x-5=2
=-23x=2+5
-23x =7
x =\(\dfrac{-7}{23}\)
x= -0.3

\(\overrightarrow{AB}=\left(3;-\dfrac{3}{2}\right)=\left(6;-3\right)=\left(2;-1\right)\)
=>VTPT là (1;2)
Phương trình AB là:
\(1\left(x+1\right)+2\left(y+\dfrac{1}{2}\right)=0\)
=>x+1+2y+1=0
=>x+2y+2=0

a)Đk \(x\ge0,x\ne1\)
\(\Rightarrow P=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)+3\left(\sqrt{x}-1\right)-6\sqrt{x}+4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x+\sqrt{x}+3\sqrt{x}-3-6\sqrt{x}+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
b)\(x=7-4\sqrt{3}=\left(2-\sqrt{3}\right)^2\Rightarrow\sqrt{x}=2-\sqrt{3}\)
\(\Rightarrow P=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}=\dfrac{2-\sqrt{3}-1}{2-\sqrt{3}+1}=\dfrac{1-\sqrt{3}}{3-\sqrt{3}}=\dfrac{-\sqrt{3}}{3}\)