K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 3 2023
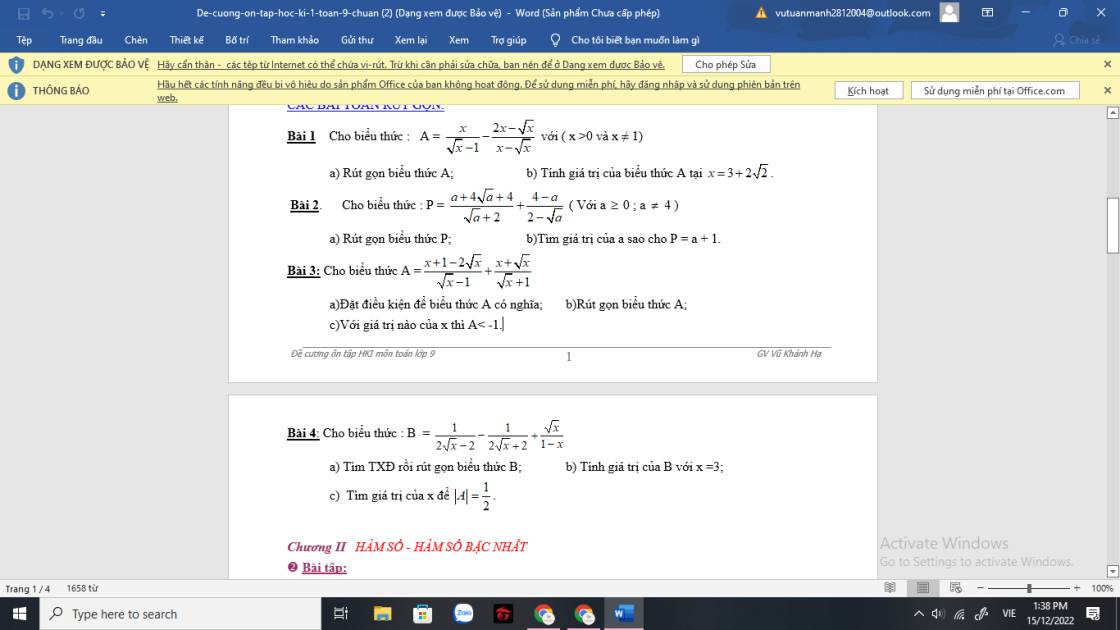
1.
a. Em tự giải
b.
\(\left\{{}\begin{matrix}2x+y=4m-1\\3x-2y=-m+9\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}4x+2y=8m-2\\3x-2y=-m+9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7x=7m+7\\y=\dfrac{3x+m-9}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m+1\\y=2m-3\end{matrix}\right.\)
Để \(x+y=7\Rightarrow m+1+2m-3=7\)
\(\Rightarrow3m=9\Rightarrow m=3\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 3 2023
2.
a. Em tự giải
b.
Phương trình có 2 nghiệm khi:
\(\Delta'=\left(m+1\right)^2-\left(2m+10\right)=m^2-9\ge0\)
\(\Rightarrow\left[{}\begin{matrix}m\ge3\\m\le-3\end{matrix}\right.\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=2m+10\end{matrix}\right.\)
Ta có:
\(P=x_1^2+x_2^2+8x_1x_2=\left(x_1+x_2\right)^2+6x_1x_2\)
\(=4\left(m+1\right)^2+6\left(2m+10\right)=4m^2+20m+64\)
\(=4\left(m^2+5m+6\right)+40=4\left(m+2\right)\left(m+3\right)+40\)
Do \(\left[{}\begin{matrix}m\ge3\\m\le-3\end{matrix}\right.\) \(\Rightarrow\left(m+2\right)\left(m+3\right)\ge0\)
\(\Rightarrow P\ge40\)
Vậy \(P_{min}=40\) khi \(m=-3\)
(Nếu bài này giải là \(4m^2+20m+64=\left(2m+5\right)^2+39\ge39\) là sai vì dấu = khi đó xảy ra tại \(m=-\dfrac{5}{2}\) ko thỏa mãn điều kiện \(\Delta\) để pt có nghiệm)
PD
1
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 1 2024
Gọi số xe dự định tham gia chở hàng là x (xe) với x>4, x nguyên dương
Mỗi xe dự định chở khối lượng hàng là: \(\dfrac{20}{x}\) (tấn)
Số xe thực tế tham gia chở hàng là: \(x-4\) (xe)
Thực tế mỗi xe phải chở số hàng là: \(\dfrac{20}{x-4}\) (tấn)
Do thực tế mỗi xe phải chở nhiều hơn dự định là 5/6 tấn hàng nên ta có pt:
\(\dfrac{20}{x-4}-\dfrac{20}{x}=\dfrac{5}{6}\)
\(\Rightarrow24x-24\left(x-4\right)=x\left(x-4\right)\)
\(\Leftrightarrow x^2-4x-96=0\)
\(\Rightarrow\left[{}\begin{matrix}x=12\\x=-8\left(loại\right)\end{matrix}\right.\)
Vậy thực tế có \(12-4=8\) xe tham gia vận chuyển
NT
0
.png)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
15 tháng 12 2022
Mình không thấy câu nào cả thì giúp kiểu gì lỗi ảnh hay sao ý
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 1 2024
ĐKXĐ: \(x+2y\ne0\)
\(\left\{{}\begin{matrix}x-\dfrac{1}{x+2y}=\dfrac{7}{4}\\-\dfrac{5}{2}x+2+\dfrac{4}{x+2y}=-2\end{matrix}\right.\)
Đặt \(\dfrac{1}{x+2y}=z\) ta được hệ:
\(\left\{{}\begin{matrix}x-z=\dfrac{7}{4}\\-\dfrac{5}{2}x+4z=-4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\z=\dfrac{1}{4}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\\\dfrac{1}{x+2y}=\dfrac{1}{4}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\x+2y=4\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)