
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: Ta có: \(\dfrac{3x-1}{2}=\dfrac{2x-2}{3}\)
\(\Leftrightarrow9x-3=4x-4\)
\(\Leftrightarrow x=-\dfrac{1}{5}\)
\(a,\Leftrightarrow\dfrac{2}{3}\left(3x-2\right)+\dfrac{4}{9}\left(3x-5\right)=-2x+1\\ \Leftrightarrow2x-\dfrac{4}{3}+\dfrac{4}{3}x-\dfrac{20}{9}+2x-1=0\\ \Leftrightarrow\dfrac{16}{3}x=\dfrac{41}{9}\Leftrightarrow x=\dfrac{41}{9}\cdot\dfrac{3}{16}=\dfrac{41}{48}\\ b,\Leftrightarrow3\left(3x-1\right)=2\left(2x-2\right)\\ \Leftrightarrow9x-3=4x-4\\ \Leftrightarrow5x=-1\Leftrightarrow x=-\dfrac{1}{5}\\ c,\Leftrightarrow15-2\left(x^2+1\right)=7\\ \Leftrightarrow13-2x^2=7\Leftrightarrow x^2=3\Leftrightarrow x=\pm\sqrt{3}\)
\(d,\Leftrightarrow x+1=\sqrt{x+1}\left(x\ge-1\right)\\ \Leftrightarrow x^2+2x+1=x+1\\ \Leftrightarrow x^2-x=0\\ \Leftrightarrow x\left(x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=1\left(tm\right)\end{matrix}\right.\)



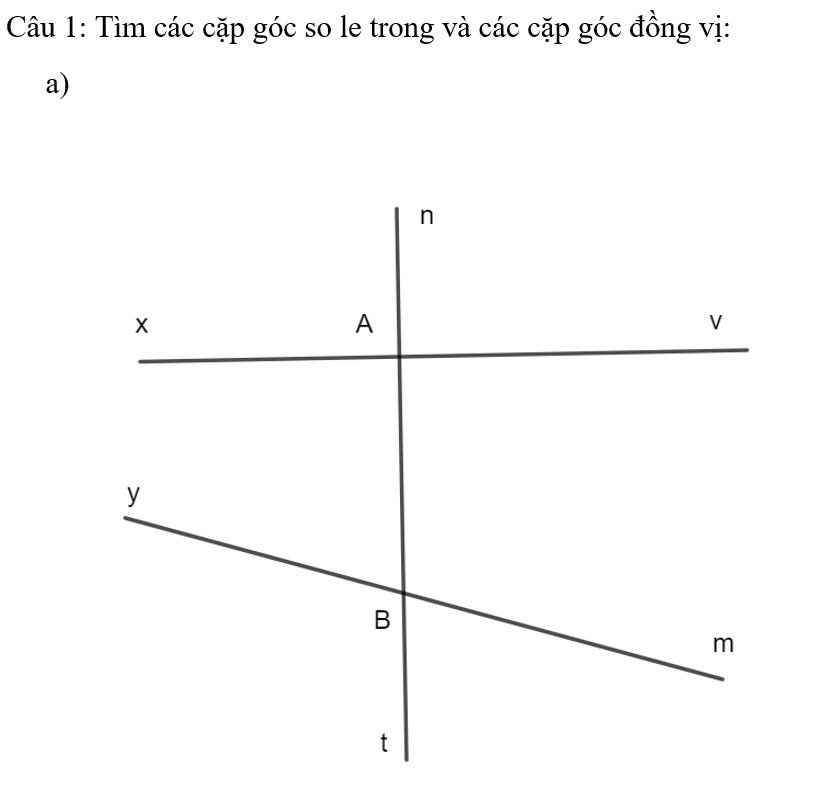
a: So le trong: góc vAB và góc yBA; góc xAB và góc mBA
ĐỒng vị: góc nAx và góc yBA; góc nAv và góc mBA; góc xAB và góc tBy; góc vAB và góc mBt
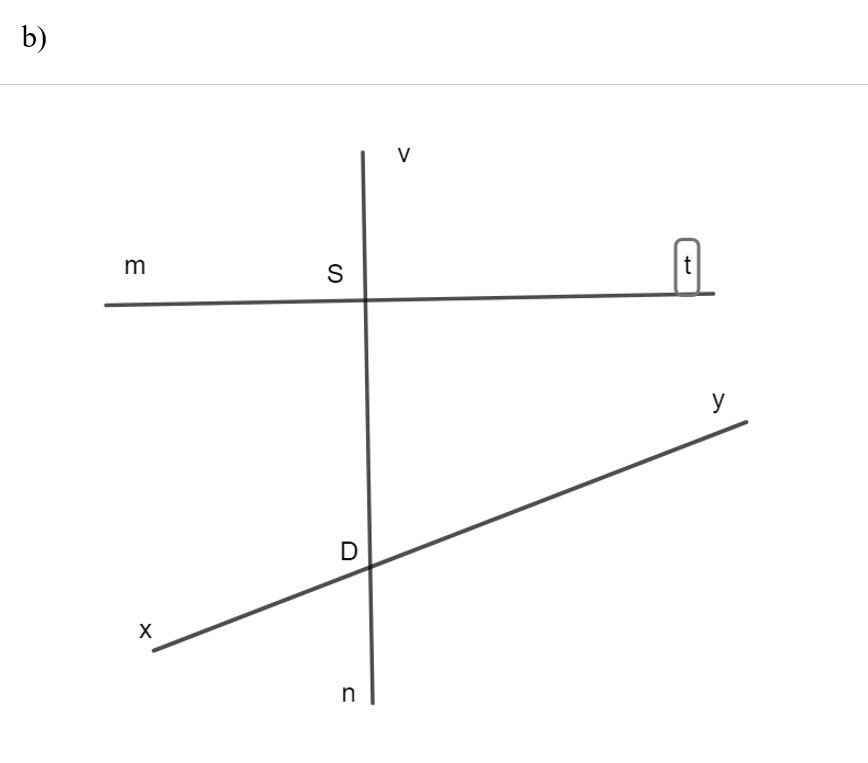
b: So le trong: góc mSD và góc yDS; góc tSD và góc xDS
ĐỒng vị: góc vSm và góc xDv; góc vSt và góc vDy; góc mSn và góc xDn; góc tSD và góc yDn
a)Cặp so le trong: xAB và ABm, vAB và ABy
Cặp đồng vị: nAx và ABy, nAv và ABm, xAB và yBt,vAB và mBt
b)Cặp so le trong: mSD và SDy, tSD và SDx
Cặp đồng vị: vSm và SDx, vSt và SDy, nDx và DSm,nDy và DSt


Đây là bài bạn phải nộp cho thầy nên mình sẽ không làm chi tiết. Nhưng mình có thể gợi ý cho bạn như sau:
1.
Đối với tỉ lệ thức đã cho, mỗi phân số ta nhân cả tử và mẫu với 4, 3, 2. Khi đó, ta thu được 1 tỉ lệ thức mới
Dùng tỉ lệ thức trên, áp dụng tính chất dãy tỉ số bằng nhau (cộng), ta thu được $12x=8y=6z(*)$
Tiếp tục áp dụng tính chất dãy tỉ số bằng nhau cho $(*)$ dựa theo điều kiện $x+y+z=18$ ta sẽ tính được $x,y,z$ thỏa mãn.
2.
Áp dụng tính chất dãy tỉ số bằng nhau (cộng) cho 3 phân số đầu tiên, ta sẽ tìm được tổng $x+y+z$
Khi tìm được tổng $x+y+z$, cộng vào 3 phân số đầu tiên trong bài, mỗi phân số cộng thêm 1. Khi đó, ta thu được tỉ lệ thức $\frac{m}{x}=\frac{n}{y}=\frac{p}{z}(*)$ với $m,n,p$ đã tính được dựa theo giá trị $x+y+z$.
Áp dụng tính chất dãy tỉ số bằng nhau cho tỉ lệ thức $(*)$, kết hợp với kết quả $x+y+z$ thì bài toán đã rất quen thuộc rồi.


Câu 8:
a. Với $x,y$ là số nguyên thì $x, y-3$ cũng là số nguyên. Mà $x(y-3)=15$ nên ta có các TH:
TH1: $x=1, y-3=15\Rightarrow x=1; y=18$ (tm)
TH2: $x=-1, y-3=-15\Rightarrow x=-1; y=-12$ (tm)
TH3: $x=15; y-3=1\Rightarrow x=15; y=4$ (tm)
TH4: $x=-15; y-3=-1\Rightarrow x=-15; y=2$ (tm)
TH5: $x=3, y-3=5\Rightarrow x=3; y=8$ (tm)
TH6: $x=-3; y-3=-5\Rightarrow x=-3; y=-2$ (tm)
TH7: $x=5; y-3=3\Rightarrow x=5; y=6$ (tm)
TH8: $x=-5; y-3=-3\Rightarrow x=-5; y=0$ (tm)
Câu 8:
b.
$xy-2y+3(x-2)=7$
$\Rightarrow y(x-2)+3(x-2)=7$
$\Rightarrow (x-2)(y+3)=7$
Do $x,y$ nguyên nên $x-2, y+3$ nguyên. Mà tích của chúng bằng $7$ nên ta có các TH sau:
TH1: $x-2=1, y+3=7\Rightarrow x=3; y=4$ (tm)
TH2: $x-2=-1; y+3=-7\Rightarrow x=1; y=-10$ (tm)
TH3: $x-2=7, y+3=1\Rightarrow x=9; y=-2$ (tm)
TH4: $x-2=-7; y+3=-1\Rightarrow x=-5; y=-4$ (tm)

\(\text{#TNam}\)
`5,A`
Gọi các cạnh của Tam giác `ABC` lần lượt là `x,y,z (x,y,z \ne 0)`
`3` góc của tam giác lần lượt tỉ lệ với `2:3:4`
Nghĩa là: `x/2=y/3=z/4`
Tổng số đo `3` góc trong `1` tam giác là `180^0`
`-> x+y+z=180`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/2=y/3=z/4=`\(\dfrac{x+y+z}{2+3+4}=\dfrac{180}{9}=20\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{2}=20\\\dfrac{y}{3}=20\\\dfrac{z}{4}=20\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=20\cdot2=40\\y=20\cdot3=60\\z=20\cdot4=80\end{matrix}\right.\)
Vậy, độ dài các cạnh của Tam giác `ABC` lần lượt là `40^0, 60^0, 80^0`.
`6,B`
Gọi số người thợ của `3` nhóm lần lượt là `x,y,z (x,y,z \ne 0)`
Vì năng suất làm việc của các người thợ như nhau `->` số thợ và số ngày là `2` đại lượng tỉ lệ nghịch
`-> 40x=60y=50z` hay \(\dfrac{x}{\dfrac{1}{40}}=\dfrac{y}{\dfrac{1}{60}}=\dfrac{z}{\dfrac{1}{50}}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{\dfrac{1}{40}}=\dfrac{y}{\dfrac{1}{60}}=\dfrac{z}{\dfrac{1}{50}}=\dfrac{x-z}{\dfrac{1}{40}-\dfrac{1}{50}}=\dfrac{3}{\dfrac{1}{200}}=600\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{\dfrac{1}{40}}=600\\\dfrac{y}{\dfrac{1}{60}}=600\\\dfrac{z}{\dfrac{1}{50}}=600\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=600\cdot\dfrac{1}{40}=15\\y=600\cdot\dfrac{1}{60}=10\\z=600\cdot\dfrac{1}{50}=12\end{matrix}\right.\)
Vậy, số thợ của nhóm `1,2,3` lần lượt là `15,10,12`.
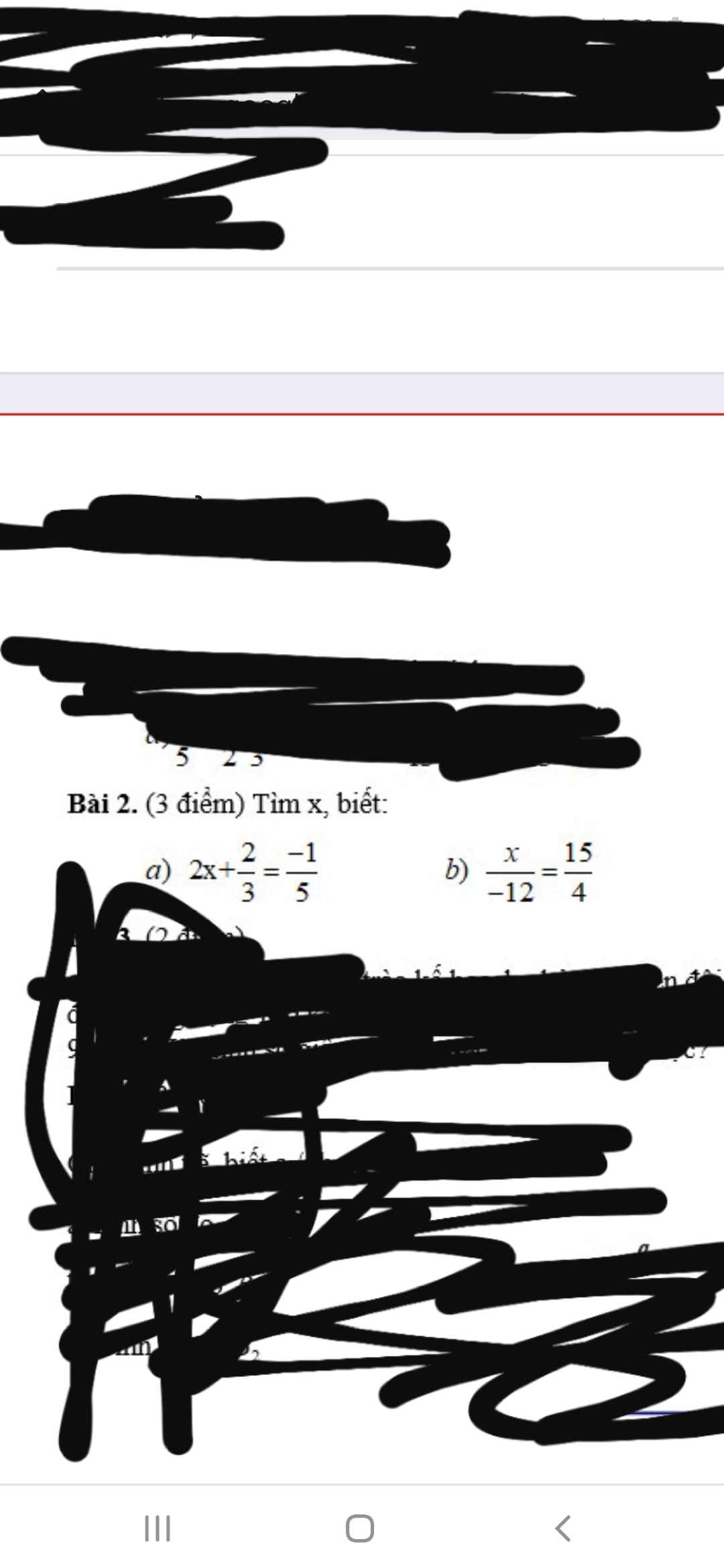
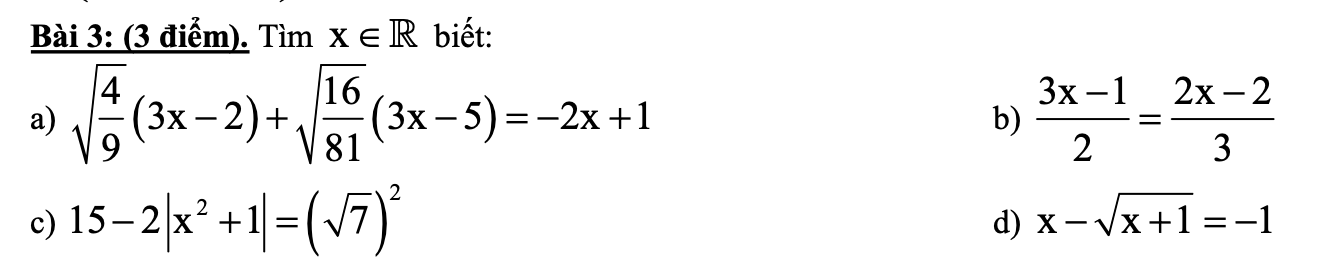

 GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP Ạ MINH CẢM ƠN RẤT NHIỀU
GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP Ạ MINH CẢM ƠN RẤT NHIỀU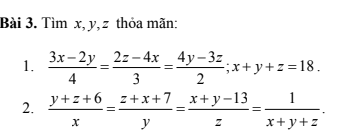
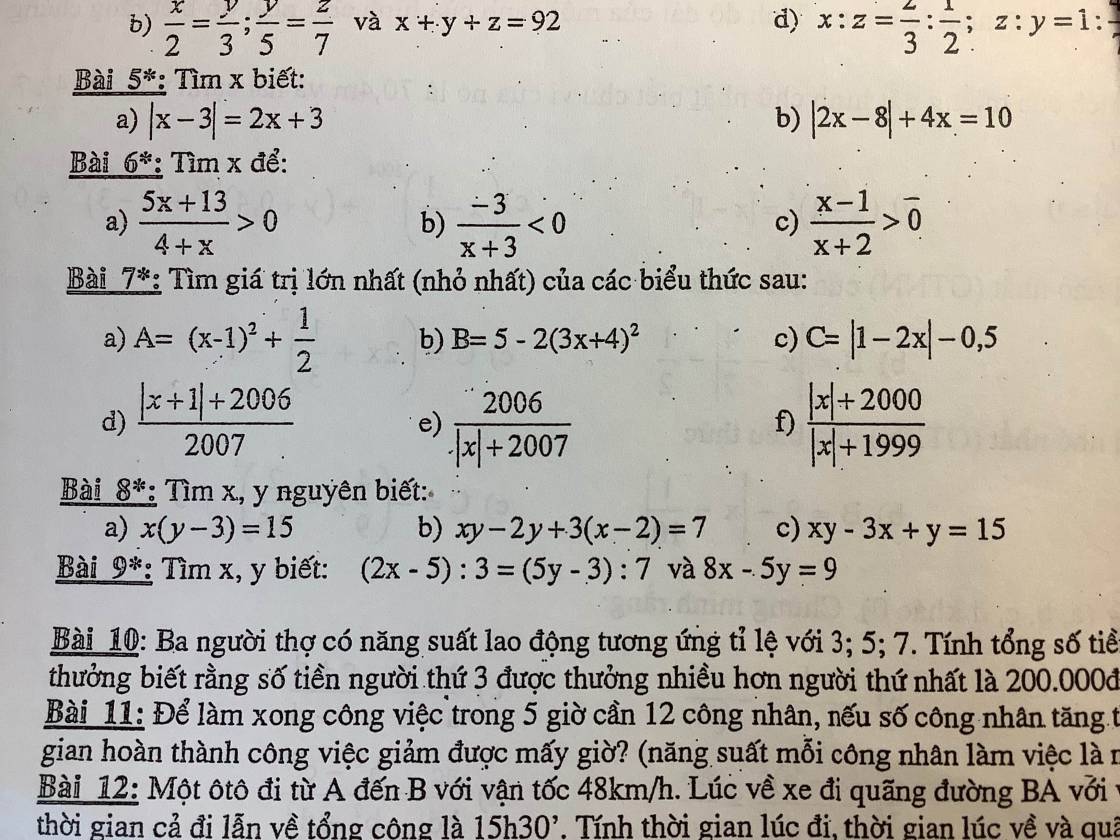

\(a,\Rightarrow2x=-\dfrac{13}{15}\Rightarrow x=-\dfrac{13}{30}\\ b,\Rightarrow x=\dfrac{-12\cdot15}{4}=-45\)