
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xét ∆AHB(<H=90°(gt)) và ∆AHC(<H=90°(gt)), ta có:
AB=AC(gt)
<B=<C(gt)
⟹∆AHB=∆AHC(c.h-g.n)
b) Xét ∆AHM(<M=90°(gt)) và ∆AHN(<N=90°(gt)), ta có:
AH cạnh chung
<MAH=NAH( vì ∆AHB=∆AHC(CM ở a))
⟹∆AHM=∆AHN(c.h-g.n)
⟹AM=AN ( 2 cạnh tương ứng)
⟹∆AMN cân tại A
c)Ta có: <M=<N=(180°-<A)/2
<B=<C=(180°-<A)/2
⟹ <M=<N=<B=<C
⟹<M=<B mà 2 góc này lại ở vị trí đồng vị
⟹MN//BC

Bài 1:
a) Áp dụng tích chất dãy tỉ số bằng nhau:
\(\dfrac{x}{2}=\dfrac{y}{3}\)=\(\dfrac{x+y}{2+3}\)=\(\dfrac{-15}{5}\)= -3
=> x= -3.2= -6; y= -3.3= -9.
b) Áp dụng tích chất dãy tỉ số bằng nhau:
\(\dfrac{x}{3}=\dfrac{y}{4}\)=\(\dfrac{x-y}{3-4}\)=\(\dfrac{12}{-1}\)= -12
=> x= -12.3= -36; y= -12.4= -48
c) 3x=7y=\(\dfrac{x}{7}=\dfrac{y}{3}\)
Áp dụng tích chất dãy tỉ số bằng nhau:
\(\dfrac{x}{y}=\dfrac{y}{3}=\dfrac{x-y}{7-3}=\dfrac{-16}{4}=-4\)
=> x= -4.7= -28; y= -4.3= -12
d) \(\dfrac{x}{y}=\dfrac{17}{13}=\dfrac{x}{17}=\dfrac{y}{13}\)
Áp dụng tích chất dãy tỉ số bằng nhau:
\(\dfrac{x}{17}=\dfrac{y}{13}=\dfrac{x+y}{17+13}=\dfrac{-60}{30}=-2\)
=> x= -2.17= -34; y= -2.13= -26
e) Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{x^2}{9}=\dfrac{y^2}{16}=\dfrac{x^2+y^2}{9+16}=\dfrac{100}{25}=4\)
=>x= 9= \(3^2\)= 3.4= 12; y= 16= \(4^2\)= 4.4= 16
Bài 2:
2x=3y=\(\dfrac{x}{3}=\dfrac{y}{2}\); 5y=7z=\(\dfrac{y}{7}=\dfrac{z}{5}\)
-> \(\dfrac{x}{3}=\dfrac{y}{2};\dfrac{y}{7}=\dfrac{z}{5}\) = \(\dfrac{x}{21}=\dfrac{y}{14};\dfrac{y}{14}=\dfrac{z}{10}\)=> \(\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{10}\) = \(\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{50}\)
Áp dụng tích chất dãy tỉ số bằng nhau:
\(\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{50}\)=\(\dfrac{3x-7y+5z}{63-98+50}\)=\(\dfrac{30}{15}=2\)
=> x= 2.21= 42
=> y= 2.14= 28
=> z= 2.10= 20


1)
a. Xét tg ABC cân tại A có AC=AB; gACB = g ABC.
Xét tg ACN và tg ABM có:
CN=BM (gt)
AC=AB
gACB=gABC
=> tg ACN = tg ABM (cgc)
=> AN=AM (2 cạnh tg ứng)
H là trung điểm BC nên AH là đường trung tuyến của tg ABC
Mak tg ABC cân => H cũng là đường cao của tg ABC => AH ⊥ BC
b. Vì H là trung đ của BC nên CH=HB=BC/2= 3cm
Áp dụng định lý Py ta go vào tg AHB có:
AB^2=AH^2+HB^2
AH^2= AB^2 - HB^2
AH^2= 5^2 - 3^2 = 16 cm
=> AH= 4 cm
c. Xét tg AMN và tg KMB có:
AM=KM (gt)
MN=BM (gt)
gHMA=gKMB (đối đỉnh)
=> tg AMN = tg KMB (cgc)
d. tg AMN = tg KMB => gMAN=gMKB
=> AN=KB=Am
Mà AB>AM (quan hệ giữ đường xiêng và hình chiếu) nên AB>BK
=> gBKA> gBAK
=> gMAN>gBAM



12:
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
=>ΔABM=ΔACM
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
b: Xét ΔNAC và ΔNBE có
góc NAC=góc NBE
NA=NB
góc ANC=góc BNE
=>ΔNAC=ΔNBE
=>AC=BE
c: Xét tứ giác AEBC có
AC//BE
AC=BE
=>AEBC là hình bình hành
=>AE//BC
d: Xét ΔEAC có EF/EA=EN/EC
nên FN//AC//EB
Xét ΔECB có CM/CB=CN/CE
nên NM//EB
=>F,N,M thẳng hàng

Hình 1 : AB//CD, CD//MN, AB// MN
Hình 2 : AN//DH, DH//MK , AN // MK
Cm
Vì góc BAC = góc MCD (=120°)
Mà 2 góc này ở vị trí slt
=> AB//CD
Vì góc MCD + góc CMN = 180° ( do 60°+120°=180°)
Mà hai góc này ở vị trí slt
=> CD // MN
Mà AB // CD ( cmt)
=> CD//AB//MN
Hình 2 : cm
Vì góc IAN = góc AID ( gt)
Mà 2 góc này ở vị trí slt
=> AN // DH
Vì góc AID = góc IKM ( gt)
Mà hai góc này ở vị trí đồng vị
=> DH // MK
Mà AN // DH ( cmt)
=> AN// DH // MK










 * Mọi người cố giúp em hoàn thiện trong buổi tối nay với ạ, em đg cần gấp! Cảm ơn ạ!
* Mọi người cố giúp em hoàn thiện trong buổi tối nay với ạ, em đg cần gấp! Cảm ơn ạ!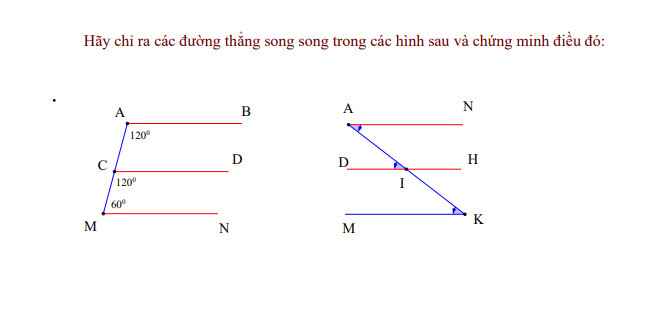
a) Ta có: \(\widehat{cNb}+\widehat{MNb}=180^{\circ}\) (hai góc kề bù)
\(\Rightarrow\widehat{MNb}=180^{\circ}-\widehat{cNb}=180^{\circ}-55^{\circ}=125^{\circ}\)
b) Ta có: \(\widehat{MNb}=\widehat{aMN}\left(=125^{\circ}\right)\)
Mà hai góc này đều nằm ở vị trí so le trong
Nên \(Ma//Nb\)