K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 10 2021
Bài 3:
a: Xét ΔADE và ΔCBF có
AD=CB
\(\widehat{A}=\widehat{C}\)
AE=CF
Do đó: ΔADE=ΔCBF
S
3 tháng 3
CÂU 1:
\(\dfrac{6x^2y^2}{8xy^5}=\dfrac{3x}{4y^3}\)
CÂU 2:
\(\dfrac{12x^3y^2}{18xy^5}=\dfrac{2x^2}{3y^3}\)
CÂU 3:
\(\dfrac{15x\left(x+5\right)^3}{20x^2\left(x+5\right)}=\dfrac{3\left(x+5\right)^2}{4x}\)
CÂU 4:
\(\dfrac{3xy+x}{9y+3}=\dfrac{x\left(3y+1\right)}{3\left(3y+1\right)}=\dfrac{x}{3}\)
CÂU 5:
\(\dfrac{3xy+3x}{9y+9}=\dfrac{3x\left(y+1\right)}{9\left(y+1\right)}=\dfrac{x}{3}\)
CÂU 6:
\(\dfrac{x^2-xy}{5y^2-5xy}=\dfrac{x\left(x-y\right)}{5y\left(y-x\right)}=\dfrac{-x\left(y-x\right)}{5y\left(y-x\right)}=\dfrac{-x}{5y}\)
CÂU 7:
\(\dfrac{2x^2+2x}{x+1}=\dfrac{2x\left(x+1\right)}{x+1}=2x\)
CÂU 8:
\(\dfrac{7x^2+14x+7}{3x^2+3x}=\dfrac{7\left(x^2+2x+1\right)}{3x\left(x+1\right)}\\ =\dfrac{7\left(x+1\right)^2}{3x\left(x+1\right)}=\dfrac{7\left(x+1\right)}{3x}\)
CÂU 9:
\(\dfrac{10xy^2\left(x+y\right)}{15xy\left(x+y\right)^3}=\dfrac{2y}{3\left(x+y\right)^2}\)
29 tháng 7 2023
a: BC=căn 6^2+8^2=10cm
bD là phân giác
=>AD/AB=CD/BC
=>AD/3=CD/5=(AD+CD)/(3+5)=8/8=1
=>AD=3cm; CD=5cm
b: Xét ΔBHA vuông tại H và ΔBAC vuông tại A có
góc B chung
=>ΔBHA đồng dạng với ΔBAC
=>BH/BA=BA/BC
=>BH*BC=BA^2
c: Xét ΔBHA có BI là phân giác
nên IH/IA=BH/BA
=>IH/IA=BA/BC=AD/DC
83
1
11 tháng 11 2021
a: Xét ΔABC có
D là trung điểm của AB
E là trung điểm của AC
Do đó: DE là đường trung bình của ΔABC
Suy ra: DE//BC
hay DECB là hình thang
26 tháng 10 2021
a: Xét tứ giác BHCD có
BH//CD
CH//BD
Do đó: BHCD là hình bình hành
16 tháng 3 2022
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó:ΔABC\(\sim\)ΔHBA
Suy ra: AB/HB=BC/BA
hay \(AB^2=HB\cdot BC\)
b: Xét ΔHAC vuông tại H và ΔHBA vuông tại H có
\(\widehat{HAC}=\widehat{HBA}\)
Do đó; ΔHAC\(\sim\)ΔHBA
SUy ra: HA/HB=HC/HA
hay \(HA^2=HB\cdot HC\)
QN
16 tháng 3 2022
a) Xét ∆ABC(<A=90 ° ) và ∆HBA(<H=90 ° ), ta có:
<B chung ⟹∆ABC~ ∆HBA(g.g)
⟹AB/HB=BC/AB⟹AB*AB=HB*BC hay AB2=BH*BC
b)Xét ∆HAC(<H=90 °) và ∆HBA(<H=90 ° ), ta được:
<B=<HAC( vì cùng phụ với <BAH do <B+<BAH =90°; <HAC+<BAH =90°)
⟹∆HAC~∆HBA(g.g)
⟹HA/HB=HC/HA⟹HA*HA=HB*HC hayHA2=BH*CH
14 tháng 10 2021
Bài 6:
a: Xét ΔABC có
D là trung điểm của BC
M là trung điểm của AC
Do đó: DM là đường trung bình của ΔABC
Suy ra: DM//AB và \(DM=\dfrac{AB}{2}=\dfrac{6}{2}=3\left(cm\right)\)
3 tháng 2 2023
a: \(A=\left(\dfrac{-\left(x+2\right)}{x-2}-\dfrac{4x^2}{\left(x-2\right)\left(x+2\right)}+\dfrac{x-2}{x+2}\right)\cdot\dfrac{x^2\left(2-x\right)}{x\left(x-3\right)}\)
\(=\dfrac{-x^2-4x-4-4x^2+x^2-4x+4}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{-x\left(x-2\right)}{x-3}\)
\(=\dfrac{-4x^2-8x}{\left(x+2\right)}\cdot\dfrac{-x}{x-3}=\dfrac{4x^2\left(x+2\right)}{\left(x+2\right)\left(x-3\right)}=\dfrac{4x^2}{x-3}\)
b: Để A chia hết cho 4 thì x^2/x-3 chia hết cho 4 và x^2 chia hết cho x-3
=>x^2/x-3=4k(k thuộc Z) và x^2-9+9 chia hết cho x-3
=>\(x-3\in\left\{1;-1;3;-3;9;-9\right\}\)
=>\(x\in\left\{4;2;6;0;12;-6\right\}\)
Kết hợp ĐK chia hết cho 4, ta được: \(x\in\left\{4;12;-6\right\}\)
NP
2
28 tháng 1 2023
a: Khi x=3 thì \(A=\dfrac{3\cdot3}{3-2}=9\)
b: C=A+B
\(=\dfrac{3x}{x-2}-\dfrac{6}{x-2}-\dfrac{x^2+4x+4}{x^2-4}\)
\(=\dfrac{3x-6}{x-2}-\dfrac{x+2}{x-2}\)
\(=\dfrac{3x-6-x-2}{x-2}=\dfrac{2x-8}{x-2}\)
c: Để C nguyên thì 2x-4-4 chia hết cho x-2
=>\(x-2\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x\in\left\{3;1;4;0;6\right\}\)
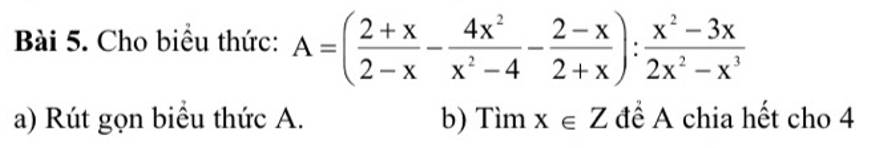
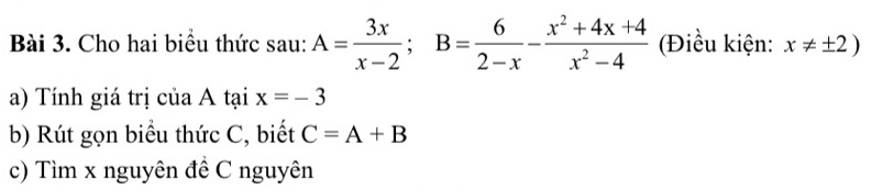
\(\Leftrightarrow4x^2-4x+4>=0\)
\(\Leftrightarrow4x^2-4x+1+3>=0\)
\(\Leftrightarrow\left(2x-1\right)^2+3>=0\)(luôn đúng)
⇔4x2−4x+4>=0⇔4x2−4x+4>=0
⇔4x2−4x+1+3>=0⇔4x2−4x+1+3>=0
⇔(2x−1)2+3>=0