TK
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
H
29 tháng 5 2023
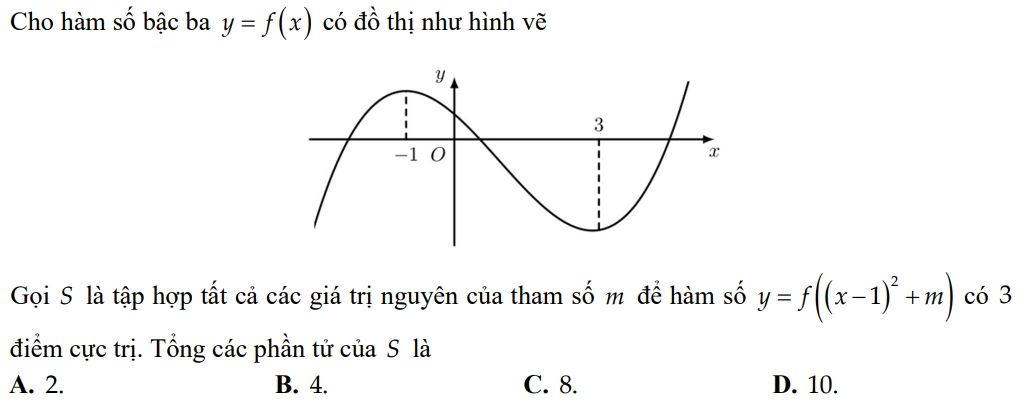
Bài này làm khá tắt chỗ 3 điểm cực trị, mình trình bày lại để bạn dễ hiểu nhé!
.......
Để y' = 0\(\Leftrightarrow\left[{}\begin{matrix}x=1\\f'\left(\left(x-1\right)^2+m\right)=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(x-1\right)^2+m=-1\\\left(x-1\right)^2+m=3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(x-1\right)^2=-1-m\left(1\right)\\\left(x-1\right)^2=3-m\left(2\right)\end{matrix}\right.\)
Để hàm số có 3 điểm cực trị thì y' = 0 có 3 nghiệm phân biệt.
Ta có 2 trường hợp.
+) \(TH_1:\) (1) có nghiệm kép x = 1 hoặc vô nghiệm và (2) có hai nghiệm phân biệt khác 1.
\(\Rightarrow\left[{}\begin{matrix}-1-m\le0\\3-m>0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m\ge-1\\m< 3\end{matrix}\right.\) \(\Leftrightarrow-1\le m< 3\)
+) \(TH_2:\) (2) có nghiệm kép x = 1 và (2) có một nghiệm phân biệt khác 1.
\(\Rightarrow\left[{}\begin{matrix}-1-m>0\\3-m\le0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m< -1\\m\ge3\end{matrix}\right.\) \(\Leftrightarrow m\in\varnothing\)
\(\Rightarrow-1\le m< 3\Rightarrow S=\left\{-1;0;1;2\right\}\)
Do đó tổng các phần tử của S là \(-1+0+1+2=2\)
ZF
2
3 tháng 10 2016
Bạn ra đáp án là bao nhiêu? Là 9 hay là 1?
Nếu ra 9 thì xin chúc mừng, bạn đã lọt vào top 60% thanh niên Nhật vừa nêu trên.
Và thực ra, họ sai vì một lầm tưởng khá phổ biến hiện nay. Logic của những người ra 9 như sau:
9 - 3 : 1/3 +1 = 9 - 3 : 1 : 3 + 1
Từ đó, vận dụng theo tính chất ưu tiên của toán học: nhân chia trước, cộng trừ sau và tính từ trái qua phải, ta sẽ có đáp án là 9.
Tuy nhiên, sự thực thì 2 phép tính này không hề giống nhau.
Hai phép tính khác nhau hoàn toàn.
Vấn đề ở đây nằm ở chỗ, khi đã viết 3 : 1/3, chúng ta phải đảm bảo rằng 1/3 luôn là một nhóm. Nói cách khác, là ta có thể viết lại phép tính như sau.
Lúc này, theo đúng tính chất ưu tiên của toán học, ta sẽ thực hiện phép tính trong ngoặc trước, sau đó đến phép chia, rồi tính cộng trừ từ trái qua phải.
Đáp án đúng sẽ là 1.
3 tháng 10 2016
Cảm ơn bn nhé, cùng Fan RinLen vs nhau cả, mk k cho bn ây^^
19 tháng 6 2016
txđ D=R
y'=-3x2+6x+3m
y' là tam thức bậc 2 nên y'=0 có tối đa 2 nghiệm
để hs nb/(0;\(+\infty\) ) thì y' \(\le\) 0 với mọi x \(\in\) (0;\(+\infty\) )
\(\Leftrightarrow\) -3x2 +6x+3m \(\le\) 0 với mọi x \(\in\) (0;\(+\infty\) )
\(\Leftrightarrow\) m\(\le\) x2 -2x với mọi x \(\in\) (0; \(+\infty\) )
xét hs g(x)=x2 -2x
g'(X) =2x-2
g'(x)=0 \(\Leftrightarrow\) x=1
vậy m \(\le\) -1
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 2 2021
\(\dfrac{d}{dx}\left(f\left(x\right)\right)\equiv f'\left(x\right)\)
\(\dfrac{1}{sinx}dx=\dfrac{sinx}{sin^2x}dx=\dfrac{sinx}{1-cos^2x}dx=\dfrac{d\left(cosx\right)}{cos^2x-1}\)
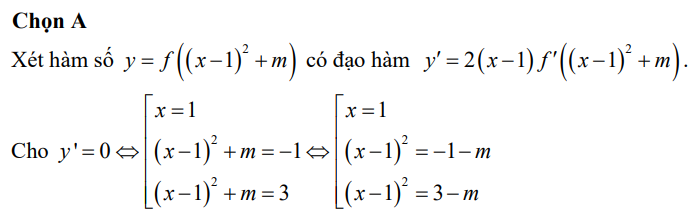
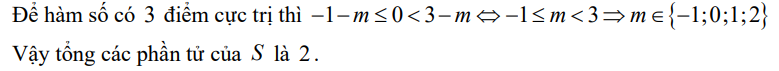
ko hiểu j ạ
Olm chào em, khi đăng câu hỏi lên diễn đàn Olm, em cần đăng đầy đủ nội dung và yêu cầu, để nhận được sự trợ giúp tốt nhất từ cộng đồng Olm em nhé. Cảm ơn em đã đồng hành cùng Olm. Chúc em học tập hiệu quả và vui vẻ cùng Olm.