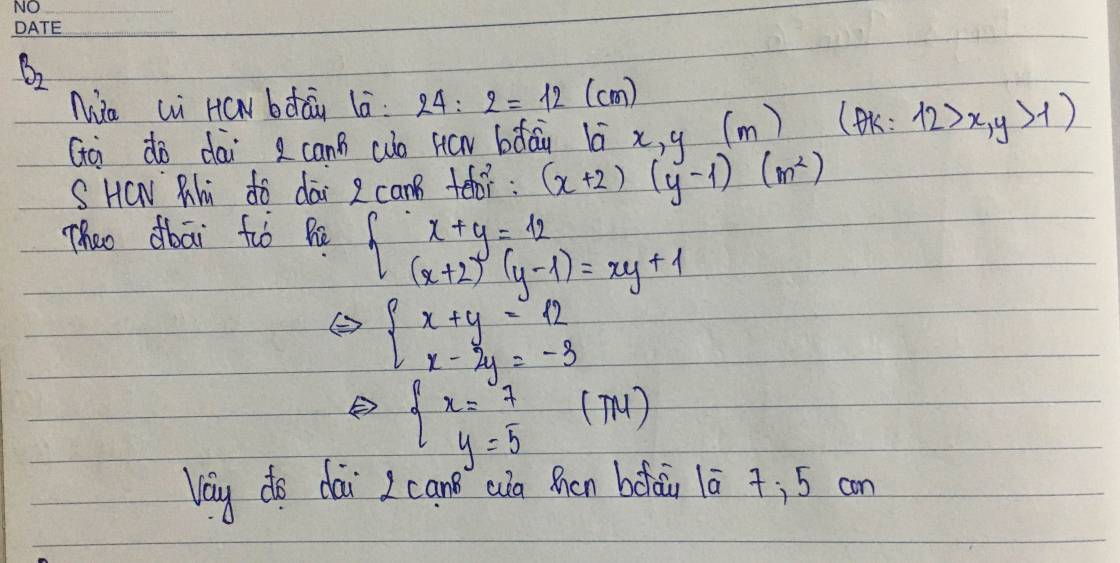Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi độ dài của mỗi cạnh của hình chữ nhật là x, và y (m)
Đk : x, y > 0
Tổng độ dài 2 cạnh là:
x + y = 24/2
=> x + y = 12 (1)
Nếu tăng độ dài 1 cạnh (x) lên 2m và giảm cạnh còn lại (y) 1m thì diện tích mảnh đất tăng thêm 1m², ta có:
(x + 2).(y - 1) = xy + 1
=> xy - x + 2y - 2 = xy + 1
=> 2y - x = 3 (2)
Từ (1) và (2), ta có hệ phương trình:
{ x + y = 12
2y - x = 3
=> { x = 12 - y
2y - x + x + y = 3 + 12
=> { x = 12 - y
3y = 15
=> { x = 7 (tm)
y = 5 (tm)
Vậy độ dài các cạnh của hình chữ nhật là 7m và 5m.

Gọi chiều dài của HCN là a; chiều rộng la b.(Đk a,b>0).
Diện tích HCN là 600 \(m^2\) : a.b=600 => b = 600/a(1)
Do thực hiện quy hoạch chung người ta cắt giảm chiều dài 10 m thì chiều dài còn lại là: a-10 nên mảnh đất trở thành hình vuông
a-10 = b(2)
Từ (1) và (2)ta có phương trình:
600/a = a - 10 <=> a^2 - 10a = 600 <=> a^2 - 10a - 600 = 0 <=> (a+20)(a-30) = 0 => a=30(thỏa mãn điều kiện) hoặc a=-20(loại vì a>0)
Vậy chiều dài và chiều rộng của HCN là 30 va 20

A B C M N P Q
a) Đặt tên các điểm như hình vẽ.
Giả sử BC = a; BM = x. Ta có MN = QP = a - 2x
Áp dụng định lý Ta let ta có:
\(\frac{AQ}{AB}=\frac{QP}{BC}\Rightarrow AQ=\frac{AB.QP}{BC}=a-2x\)
\(\Rightarrow QB=AB-AQ=a-\left(a-2x\right)=2x\)
\(\Rightarrow QM=\sqrt{QB^2-BM^2}=\sqrt{4x^2-x^2}=x\sqrt{3}\)
\(\Rightarrow S_{MNPQ}=MN.QM=\left(a-2x\right).x\sqrt{3}\)
\(=-2\sqrt{3}x^2+a\sqrt{3}x\)
\(=-2\sqrt{3}\left(x^2-2.\frac{a}{4}.x+\frac{a^2}{16}\right)+\frac{a^2\sqrt{3}}{8}\)
\(=-2\sqrt{3}\left(x-\frac{a}{4}\right)^2+\frac{a^2\sqrt{3}}{8}\le\frac{a^2\sqrt{3}}{8}\)
Vậy diện tích lớn nhất của hình chữ nhật là \(\frac{a^2\sqrt{3}}{8}\) khi BM = BC/4
b) Em tham khảo tại đây nhé.
Câu hỏi của Nguyễn Tuấn Minh - Toán lớp 8 - Học toán với OnlineMath

Pitago đảo \(\Rightarrow\Delta ABC\) vuông tại A
Ta có: \(PQ||AC\) (cùng vuông góc AB)
\(\Rightarrow\dfrac{PQ}{AC}=\dfrac{BP}{BC}\)
Tương tự: \(\dfrac{PR}{AB}=\dfrac{CP}{BC}\)
\(\Rightarrow\dfrac{PQ.PR}{AB.AC}=\dfrac{BP.CP}{BC^2}\)
\(\Rightarrow PQ.PR=\dfrac{30.40}{50^2}.BP.CP=\dfrac{12}{25}BP.CP\le\dfrac{3}{25}\left(BP+CP\right)^2=\dfrac{3}{25}.BC^2=300\)
Dấu "=" xảy ra khi \(BP=CP\) hay P là trung điểm BC
P cách B 25m

Khi quay hình chữ nhật quanh cạnh BC:
Stp trụ = 2π.AB.AD + 2π. A B 2 = S 1
Khi quay cạnh CD: Stp trụ = 2π.AB.AD + 2π. B C 2 = S 2
Mặt khác: S 1 = S 2 <=> 2π.AB.AD + 2π. A B 2 = 2π.AB.AD + 2π. B C 2
<=> AB = BC => ABCD là hình vuông

cái hình thì mk gửi link trong ib nhé
a) Gọi O là giao điểm của AC và BD
\(\Delta OAB\) vuông tại O có \(OA^2+OB^2=AB^2=49\)
Lại có: \(\tan BAC=\tan OAB=\frac{OB}{OA}=\frac{3}{4}\)\(\Leftrightarrow\)\(\frac{OA^2}{16}=\frac{OB^2}{9}=\frac{OA^2+OB^2}{16+9}=\frac{49}{25}\)
\(\Rightarrow\)\(\hept{\begin{cases}\frac{OA}{4}=\frac{7}{5}\\\frac{OB}{3}=\frac{7}{5}\end{cases}}\Leftrightarrow\hept{\begin{cases}OA=\frac{28}{5}\left(cm\right)\\OB=\frac{21}{5}\left(cm\right)\end{cases}}\)
\(\Rightarrow\)\(\hept{\begin{cases}AC=2OA=\frac{56}{5}\left(cm\right)\\BD=2OB=\frac{42}{5}\left(cm\right)\end{cases}}\)
\(\Rightarrow\)\(S_{ABCD}=\frac{1}{2}AC.BD=\frac{1}{2}.\frac{56}{5}.\frac{42}{5}=\frac{1176}{25}=47,04\left(cm^2\right)\)
b) Gọi E, F lần lược là giao điểm của BD với MN và PQ
tam giác ABD có MQ // BD
\(\Rightarrow\)\(\frac{MQ}{BD}=\frac{MA}{AB}\) ( hệ quả định lí Talet )
tam giác OAD có QF // OA
\(\Rightarrow\)\(\frac{QF}{OA}=\frac{DQ}{AQ}=\frac{MB}{AB}\) ( hệ quả định lí Talet )
\(\Rightarrow\)\(\frac{MQ}{BD}+\frac{QF}{OA}=\frac{MA+MB}{AB}=1\)
\(\Rightarrow\)\(1\ge2\sqrt{\frac{MQ.QF}{BD.OA}}\)\(\Leftrightarrow\)\(MQ.QF\le\frac{1}{4}BD.OA\)
Tương tự, ta cũng có: \(NP.PF\le\frac{1}{4}BD.OC\)
\(\Rightarrow\)\(MQ.QF+NP.PF=S_{MEFQ}+S_{NEFP}=S_{MNPQ}\le\frac{1}{4}BD.AC=\frac{1}{2}S_{ABCD}=23,52\left(cm^2\right)\)
Dấu "=" xảy ra khi M, N, P, Q là trung điểm của AB, BC, CD, DA