NN
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TL
0
TT
3
VN
18 tháng 12 2016
a) \(2^2=4\)
\(\sqrt{3^2}=3\)
\(4>3\Rightarrow\) \(2>\sqrt{3}\)
b) \(6^2=36\)
\(\sqrt{41^2}=41\)
\(36< 41\Rightarrow6< \sqrt{41}\)
TD
1
22 tháng 9 2015
Bài 41. Cho tam giác ABC, cac tia phân giác của các góc B và C cắt nhau ở I. Vẽ ID AB(D nằm trên AB), IE BC (E thuộc BC ), IF vuông góc với AC(F thuộc AC) CMR: ID=IE=IF.
Giải:
Hai tam giác vuông BID và BIE có:
BI là cạnh chung
=(gt)
nên ∆BID=∆BIE.
(cạnh huyền - góc nhọn)
Suy ra ID=IE (1)
Tương tự ∆CIE=CIF(cạnh huyền góc nhọn).
Suy ra: IE =IF (2)
Từ (1)(2) suy ra: ID=IE=IF.
LH
4 tháng 10 2017
Bài 1: ( Tự vẽ hình )
Áp dụng tỉ số lượng giác trong tam giác vuông DEF
\(TanF=\frac{DE}{DF}=\frac{3}{5}\)
\(TanF=31\)
Bài 2: ( Tự vẽ hình, gợi ý: Vẽ tam giác vuông ABC chọn góc \(\widehat{B}\)là góc \(\alpha\))
Áp dụng định lý Pytago vào tam giác vuông ABC:
\(BC^2=AC^2+AB^2\)
\(1+cot^2\alpha=1+\frac{AB^2}{AC^2}=\frac{AC^2+AB^2}{AC^2}\)
\(1+cot^2\alpha=\frac{BC^2}{AC^2}=1:\frac{AC^2}{BC^2}\)
\(1+cot^2\alpha=1:sin^2\alpha\)
\(1+cot^2\alpha=\frac{1}{sin^2\alpha}\)
KN
4
AH
Akai Haruma
Giáo viên
30 tháng 10 2021
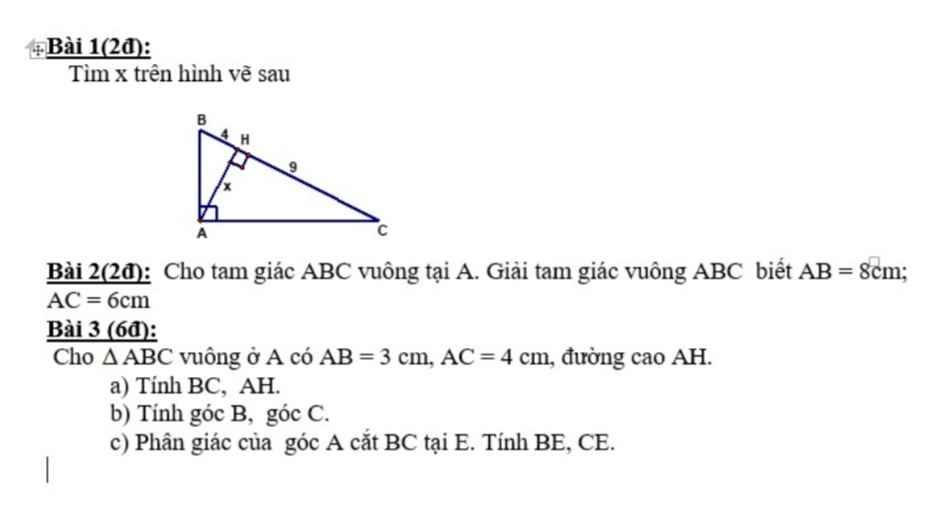
Bài 1:
Áp dụng HTL trong tam giác vuông:
$AH^2=BH.CH$
$\Leftrightarrow x^2=4.9=36$
$\Rightarrow x=6$ (do $x>0$)
AH
Akai Haruma
Giáo viên
30 tháng 10 2021
Bài 2:
Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10$ (cm)
$\sin B=\frac{AC}{BC}=\frac{6}{10}=\frac{3}{5}$
$\Rightarrow \widehat{B}=36,87^0$
$\widehat{C}=90^0-\widehat{B}=90^0-36,87^0=53,13^0$