Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp: Sử dụng lí thuyết và công thức máy biến áp
Cách giải:
Máy biến thế là thiết bị làm thay đổi điện áp xoay chiều mà không làm thay đổi tần số của nó.
Cuộn sơ cấp được nối với mạng điện 110 V – 50 Hz nên tần số của điện áp hai đầu cuộn thứ cấp cũng là 50 Hz
Vì N 1 N 2 = U 1 U 2 nên để thỏa mãn là máy tăng thế thì N2 > N1
Áp dụng công thức ta tính được điện áp hai đầu cuộn thứ cấp
N 1 N 2 = U 1 U 2 ⇒ U 2 = N 2 N 1 U 1 = 220 V

Dòng điện trễ pha hơn uAB nên X chứa cuộn cảm L'
Tổng trở của mạch \(Z=\dfrac{U}{I}=100\Omega\)
Mà \(Z=\sqrt{R^2+Z_L^2}\)
\(\Rightarrow 100=\sqrt{80^2+Z_L^2}\)
\(\Rightarrow Z_L=60\Omega\)
\(\Rightarrow L=\dfrac{0,5}{\pi}(H)\)

Chọn đáp án A
Ta có U C = I Z C ; Z C không đổi, U C đạt giá trị cực đại khi I đạt giá trị cực đại
+ Mà I = U Z = U R 2 + Z L − Z C 2
I = I max ⇒ Z = Z min ⇔ L C ω 2 = 1 ⇒ L = 1 C ω 2 = 1 10 − 4 2 π 100 2 π 2 = 0 , 637 H

u=Ucăn6sin(100πt) \(\Rightarrow U_{toanmach}=U\sqrt{3}V\) Ta thấy \(U\sqrt{3}=\sqrt{\left(U\sqrt{2}\right)^2+U^2}\) hay \(U_{mach}=\sqrt{U^2_X+U^2_Y}\)
Vậy, X chứa R. Y chứa L hoặc C.
Hoặc ngược lại

+ Khi $\lambda _1=10m :$ Từ $\lambda _1=2\pi c\sqrt{LC_1} $
$\Rightarrow C_1=\frac{\lambda _1}{4\pi^2c^2L} =3,2.10^{-13} F=0,32 pF$
Do $C_1 < C_0$ nên cần ghép tụ xoay $C_x$ nối tiếp tụ $C_0$ với $\frac{1}{C_1}=\frac{1}{C_x} +\frac{1}{C_0}\Rightarrow C_x\approx 0,32 pF $
+ Khi $\lambda _2=50m : $ Từ $\lambda _2=2\pi c\sqrt{LC_2} \Rightarrow C_2=\frac{\lambda _2}{4\pi^2c^2L} =1,6.10^{-12}F=1,6 pF $
Do $C_2 < C_0$ nên cần ghép tụ xoay $C'_x$ nối tiếp tụ $C_0$ với $\frac{1}{C_2}=\frac{1}{C'_x}+\frac{2}{C_0}\Rightarrow C'_x\approx 1,6 pF$
Vậy cần ghép tụ xoay nối tiếp với tụ $C_0$ với giá trị từ $0,32 pF$ đến $1,6 pF$
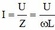

Help me
Điện áp sinh ra ở cuộn thứ cấp là: 220 : 10 = 22 (V)
Điện trở của mạch thứ cấp là: 2 + 20 = 22 (ôm)
Cường độ dòng điện mạch thứ cấp: I = 22 : 22 = 1 (A)
Điện áp hiệu dụng cuộn thứ cấp: 1 . 20 = 20(V)