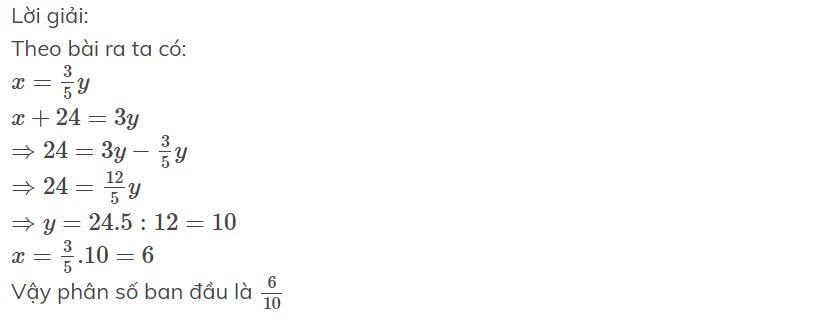Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi a và b lần lượt là tử số và mẫu số của phân số ban đầu
nên ta có :\(\frac{a}{b}=\frac{5}{7}\)hay a.7=b.5
\(\Rightarrow\)\(\frac{a}{5}=\frac{b}{7}\)
Áp dụng định lí của dãy tỷ số bằng nhau ta có:
\(\frac{a}{5}=\frac{b}{7}=\frac{a+b}{5+7}=\frac{4812}{12}=401\)
Nếu \(\frac{a}{5}=401\)\(\Rightarrow a=401.5=2005\)
Nếu \(\frac{b}{7}=401\Rightarrow b=401.7=2807\)
Vậy phân số ban đầu là\(\frac{2005}{2807}\)

Lời giải:
Theo bài ra ta có:
$x=\frac{3}{5}y$
$x+24=3y$
$\Rightarrow 24=3y-\frac{3}{5}y$
$\Rightarrow 24 = \frac{12}{5}y$
$\Rightarrow y=24.5:12=10$
$x=\frac{3}{5}.10=6$
Vậy phân số ban đầu là $\frac{6}{10}$

Gọi mẫu số của phân số cần tìm là x ( x khác 0 )
=> Tử số của phân số cần tìm là x - 7
=> Phân số cần tìm có dạng \(\frac{x-7}{x}\)
Thêm cả tử và mẫu 5 đơn vị thì được phân số mới = 1/2
=> Ta có phương trình : \(\frac{x-7+5}{x+5}=\frac{1}{2}\)
<=> \(\frac{x-2}{x+5}=\frac{1}{2}\)
<=> 2( x - 2 ) = x + 5
<=> 2x - 4 = x + 5
<=> 2x - x = 5 + 4
<=> x = 9 ( tmđk )
=> Mẫu số của phân số ban đầu là 9

Gọi tử số là : a ; mẫu số là b
Theo bài ra ta có : b - a = 25 (1 ) và \(\frac{a+3}{b-7}=\frac{1}{6}\)(2)
Từ (1) ta có : \(b-a=25\Rightarrow a=b-25\)
Thay vào (2) : \(\frac{b-25+3}{b-7}=\frac{1}{6}\Leftrightarrow\frac{b-22}{b-7}=\frac{1}{6}\)
\(\Rightarrow6b-132=b-7\Leftrightarrow5b=125\Leftrightarrow b=25\)
Suy ra : \(a=25-25=0\)
Vậy phân số cần tìm là \(\frac{a}{b}=\frac{0}{25}=0\)