Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(=\lim\limits_{x\rightarrow+\infty}\dfrac{4+\dfrac{3}{x}}{2}=\dfrac{4}{2}=2\)
b: \(=\lim\limits_{x\rightarrow-\infty}\dfrac{\dfrac{2}{x}}{3+\dfrac{1}{x}}=0\)
c: \(=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{1+\dfrac{1}{x^2}}}{1+\dfrac{1}{x}}=1\)

a: \(\lim\limits_{x\rightarrow-1^+}x+1=0\)
=>\(\lim\limits_{x\rightarrow-1^+}\dfrac{1}{x+1}=+\infty\)
b: \(\lim\limits_{x\rightarrow-\infty}1-x^2=\lim\limits_{x\rightarrow-\infty}\left[x^2\left(\dfrac{1}{x^2}-1\right)\right]\)
\(=-\infty\)
c: \(\lim\limits_{x\rightarrow3^-}\dfrac{x}{3-x}=\lim\limits_{x\rightarrow3^-}=\dfrac{-x}{x-3}\)
\(\lim\limits_{x\rightarrow3^-}x-3=0\)
\(\lim\limits_{x\rightarrow3^-}-x=3>0\)
=>\(\lim\limits_{x\rightarrow3^-}\dfrac{x}{3-x}=+\infty\)

a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{9x + 1}}{{3x - 4}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{x\left( {9 + \frac{1}{x}} \right)}}{{x\left( {3 - \frac{4}{x}} \right)}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{9 + \frac{1}{x}}}{{3 - \frac{4}{x}}} = \frac{{9 + 0}}{{3 - 0}} = 3\)
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{7x - 11}}{{2x + 3}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{x\left( {7 - \frac{{11}}{x}} \right)}}{{x\left( {2 + \frac{3}{x}} \right)}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{7 - \frac{{11}}{x}}}{{2 + \frac{3}{x}}} = \frac{{7 - 0}}{{2 + 0}} = \frac{7}{2}\)
c) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {{x^2} + 1} }}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{x\sqrt {1 + \frac{1}{{{x^2}}}} }}{x} = \mathop {\lim }\limits_{x \to + \infty } \sqrt {1 + \frac{1}{{{x^2}}}} = \sqrt {1 + 0} = 1\)
d) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^2} + 1} }}{x} = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - x\sqrt {1 + \frac{1}{{{x^2}}}} }}{x} = \mathop {\lim }\limits_{x \to - \infty } - \sqrt {1 + \frac{1}{{{x^2}}}} = - \sqrt {1 + 0} = - 1\)
e) Ta có: \(\left\{ \begin{array}{l}1 > 0\\x - 6 < 0,x \to {6^ - }\end{array} \right.\)
Do đó, \(\mathop {\lim }\limits_{x \to {6^ - }} \frac{1}{{x - 6}} = - \infty \)
g) Ta có: \(\left\{ \begin{array}{l}1 > 0\\x + 7 > 0,x \to {7^ + }\end{array} \right.\)
Do đó, \(\mathop {\lim }\limits_{x \to {7^ + }} \frac{1}{{x - 7}} = + \infty \)

a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{1 - 3{x^2}}}{{{x^2} + 2x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2}\left( {\frac{1}{{{x^2}}} - 3} \right)}}{{{x^2}\left( {1 + \frac{{2x}}{{{x^2}}}} \right)}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{1}{{{x^2}}} - 3}}{{1 + \frac{2}{x}}} = \frac{{\mathop {\lim }\limits_{x \to + \infty } \frac{1}{{{x^2}}} - \mathop {\lim }\limits_{x \to + \infty } 3}}{{\mathop {\lim }\limits_{x \to + \infty } 1 + \mathop {\lim }\limits_{x \to + \infty } \frac{2}{x}}} = \frac{{0 - 3}}{{1 + 0}} = - 3\)
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{2}{{x + 1}} = \mathop {\lim }\limits_{x \to - \infty } \frac{2}{{x\left( {1 + \frac{1}{x}} \right)}} = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x}.\mathop {\lim }\limits_{x \to - \infty } \frac{2}{{1 + \frac{1}{x}}} = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x}.\frac{{\mathop {\lim }\limits_{x \to - \infty } 2}}{{\mathop {\lim }\limits_{x \to - \infty } 1 + \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x}}} = 0.\frac{2}{{1 + 0}} = 0\).

a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{ - x + 2}}{{x + 1}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{x\left( { - 1 + \frac{2}{x}} \right)}}{{x\left( {1 + \frac{1}{x}} \right)}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 1 + \frac{2}{x}}}{{1 + \frac{1}{x}}} = \frac{{\mathop {\lim }\limits_{x \to + \infty } \left( { - 1} \right) + \mathop {\lim }\limits_{x \to + \infty } \frac{2}{x}}}{{\mathop {\lim }\limits_{x \to + \infty } 1 + \mathop {\lim }\limits_{x \to + \infty } \frac{1}{x}}} = \frac{{ - 1 + 0}}{{1 + 0}} = - 1\)
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{x - 2}}{{{x^2}}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{x\left( {1 - \frac{2}{x}} \right)}}{{{x^2}}} = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x}.\mathop {\lim }\limits_{x \to - \infty } \left( {1 - \frac{2}{x}} \right)\)
\( = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x}.\left( {\mathop {\lim }\limits_{x \to - \infty } 1 - \mathop {\lim }\limits_{x \to - \infty } \frac{2}{x}} \right) = 0.\left( {1 - 0} \right) = 0\).

a) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{6x + 8}}{{5x - 2}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{x\left( {6 + \frac{8}{x}} \right)}}{{x\left( {5 - \frac{2}{x}} \right)}} = \frac{6}{5}\)
b) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{6x + 8}}{{5x - 2}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{x\left( {6 + \frac{8}{x}} \right)}}{{x\left( {5 - \frac{2}{x}} \right)}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{6 + \frac{8}{x}}}{{5 - \frac{2}{x}}} = \frac{6}{5}\).
c) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {9{x^2} - x + 1} }}{{3x - 2}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - x\sqrt {9 - \frac{1}{x} + \frac{1}{{{x^2}}}} }}{{x\left( {3 - \frac{2}{x}} \right)}} = - \frac{3}{3} = - 1\).
d) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {9{x^2} - x + 1} }}{{3x - 2}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{x\sqrt {9 - \frac{1}{x} + \frac{1}{{{x^2}}}} }}{{x\left( {3 - \frac{2}{x}} \right)}} = \frac{3}{3} = 1\).
e) \(\mathop {\lim }\limits_{x \to - {2^ - }} \frac{{3{x^2} + 4}}{{2x + 4}} = - \infty \)
Do \(\mathop {\lim }\limits_{x \to - {2^ - }} \left( {3{x^2} + 1} \right) = 3.{\left( { - 2} \right)^2} + 1 = 13 > 0\) và \(\mathop {\lim }\limits_{x \to - {2^ - }} \frac{1}{{2x + 4}} = - \infty \)
g) \(\mathop {\lim }\limits_{x \to - {2^ + }} \frac{{3{x^2} + 4}}{{2x + 4}} = + \infty \).
Do \(\mathop {\lim }\limits_{x \to - {2^ + }} \left( {3{x^2} + 1} \right) = 3.{\left( { - 2} \right)^2} + 1 = 13 > 0\) và \(\mathop {\lim }\limits_{x \to - {2^ + }} \frac{1}{{2x + 4}} = + \infty \)

a) \(\mathop {\lim }\limits_{x \to {3^ - }} \frac{{2x}}{{x - 3}} = \mathop {\lim }\limits_{x \to {3^ - }} \left( {2x} \right).\mathop {\lim }\limits_{x \to {3^ - }} \frac{1}{{x - 3}}\)
Ta có: \(\mathop {\lim }\limits_{x \to {3^ - }} \left( {2x} \right) = 2\mathop {\lim }\limits_{x \to {3^ - }} x = 2.3 = 6;\mathop {\lim }\limits_{x \to {3^ - }} \frac{1}{{x - 3}} = - \infty \)
\( \Rightarrow \mathop {\lim }\limits_{x \to {3^ - }} \frac{{2x}}{{x - 3}} = - \infty \)
b) \(\mathop {\lim }\limits_{x \to + \infty } \left( {3x - 1} \right) = \mathop {\lim }\limits_{x \to + \infty } x\left( {3 - \frac{1}{x}} \right) = \mathop {\lim }\limits_{x \to + \infty } x.\mathop {\lim }\limits_{x \to + \infty } \left( {3 - \frac{1}{x}} \right)\)
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } x = + \infty ;\mathop {\lim }\limits_{x \to + \infty } \left( {3 - \frac{1}{x}} \right) = \mathop {\lim }\limits_{x \to + \infty } 3 - \mathop {\lim }\limits_{x \to + \infty } \frac{1}{x} = 3 - 0 = 3\)
\( \Rightarrow \mathop {\lim }\limits_{x \to + \infty } \left( {3x - 1} \right) = + \infty \)

Bài 1:
\(a=\lim\limits_{x\rightarrow-\infty}\frac{2\left|x\right|+1}{3x-1}=\lim\limits_{x\rightarrow-\infty}\frac{-2x+1}{3x-1}=\lim\limits_{x\rightarrow-\infty}\frac{-2+\frac{1}{x}}{3-\frac{1}{x}}=-\frac{2}{3}\)
\(b=\lim\limits_{x\rightarrow+\infty}\frac{\sqrt{9+\frac{1}{x}+\frac{1}{x^2}}-\sqrt{4+\frac{2}{x}+\frac{1}{x^2}}}{1+\frac{1}{x}}=\frac{\sqrt{9}-\sqrt{4}}{1}=1\)
\(c=\lim\limits_{x\rightarrow+\infty}\frac{\sqrt{1+\frac{2}{x}+\frac{3}{x^2}}+4+\frac{1}{x}}{\sqrt{4+\frac{1}{x^2}}+\frac{2}{x}-1}=\frac{1+4}{\sqrt{4}-1}=5\)
\(d=\lim\limits_{x\rightarrow+\infty}\frac{\frac{3}{x}-\frac{2}{x\sqrt{x}}+\sqrt{1-\frac{5}{x^3}}}{2+\frac{4}{x}-\frac{5}{x^2}}=\frac{1}{2}\)
Bài 2:
\(a=\lim\limits_{x\rightarrow-\infty}\frac{2+\frac{1}{x}}{1-\frac{1}{x}}=2\)
\(b=\lim\limits_{x\rightarrow-\infty}\frac{2+\frac{3}{x^3}}{1-\frac{2}{x}+\frac{1}{x^3}}=2\)
\(c=\lim\limits_{x\rightarrow+\infty}\frac{x^2\left(3+\frac{1}{x^2}\right)x\left(5+\frac{3}{x}\right)}{x^3\left(2-\frac{1}{x^3}\right)x\left(1+\frac{4}{x}\right)}=\frac{15}{+\infty}=0\)

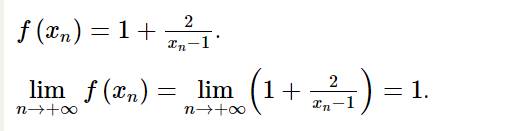
\(\mathop {\lim }\limits_{x \to + \infty } \frac{{2{\rm{x}} - 1}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{x\left( {2 - \frac{1}{x}} \right)}}{x} = \mathop {\lim }\limits_{x \to + \infty } \left( {2 - \frac{1}{x}} \right) = 2 - 0 = 2\)
Chọn A.