Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng công thức:
$P_1=\dfrac{U^2}{R_1}\cos ^2\varphi _1$ và $P_2=\dfrac{U^2}{R_2}\cos ^2\varphi _2$
$\Leftrightarrow 60=\dfrac{100^2}{50}\cos ^2\varphi _1\Leftrightarrow \cos ^2\varphi _1=\dfrac{3}{10}$
$\Leftrightarrow \cos ^2\varphi _2=\dfrac{9}{20}$
$\Leftrightarrow P_2=180$
$\dfrac{P_2}{P_1}=3$

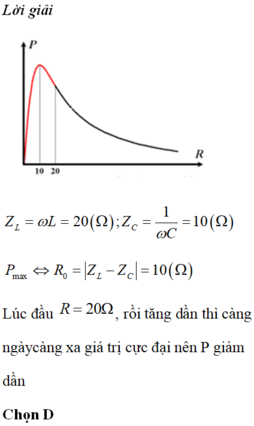
Ta có Z L − Z C = 10 Ω.
→ Khi tăng biến trở R từ giá trị R = 20 Ω thì công suất tiệu thụ luôn giảm.
Đáp án D

Để cường độ dòng điện trong mạch đạt cực đại thì cần điều chỉnh tần số đến giá trị \(f_0\)
\(\Rightarrow f_0=\sqrt{f_1.f_2}=\sqrt{25.100}=50(hz)\)

Ta áp dụng kết quả sau:
Mạch RLC có R thay đổi, khi R = R1 hoặc R = R2 thì công suất của mạch như nhau là P, khi đó:
\(\begin{cases}R_1+R_2=\frac{U^2}{P}\\R_1R_2=\left(Z_L-Z_C\right)^2\end{cases}\)
\(\Rightarrow R_1R_2=Z_C^2=100^2\)(1)
Điện áp hiệu dụng giữa hai đầu tụ điện: \(U_C=IZ_C=\frac{U.Z_C}{\sqrt{R^2+Z_C^2}}\)
\(U_{C1}=2U_{C2}\)
\(\Rightarrow\frac{U.Z_C}{\sqrt{R_1^2+Z_C^2}}=\frac{2U.Z_C}{\sqrt{R^2_2+Z_C^2}}\)
\(\Rightarrow2\sqrt{R_1^2+Z_C^2}=\sqrt{R_2^2+Z_C^2}\)
\(\Rightarrow4\left(R_1^2+100^2\right)=\left(R_2^2+100^2\right)\)
\(\Rightarrow4R_1^2-R_2^2=-3.100^2\)
Rút R2 ở (1) thế vào pt trên ta đc:
\(4R_1^2-\frac{100^4}{R_1^2}=-3.100^2\)
\(\Rightarrow4R_1^4+3.100^2.R_1^2-100^4=0\)
\(\Rightarrow R_1=50\Omega\)
\(\Rightarrow R_2=20\Omega\)

Đáp án: D
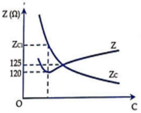
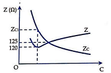
Trên đồ thị ta có:
Tại C1 thì Z m i n = R = 120 Ω , Khi đó Z C 1 = Z L .
Gọi C2 theo đồ thị thì Z = Z C 2 = 125 Ω :
Z = R 2 + Z L - Z C 2 → 125 2 = 120 2 + Z L - Z C 2 2 .
⇒ 125 2 = 120 2 + Z L - 125 2
⇒ Z L = 90 Ω (loại) hoặc Z L = 160 Ω = Z C 1
⇒
Tại
C
1
:
I
m
i
n
=
U
Z
m
i
n
=
U
R
=
150
120
=
1
,
25
A
Điện áp hiệu dụng giữa hai bản tụ điện: U C = I . Z C 1 = 1 , 25 . 160 = 200 V
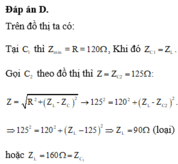
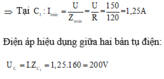

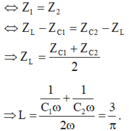
Ta có: \(U_R=I.R=\dfrac{U.R}{\sqrt{R^2+(Z_L-Z_C)^2}}\)
Để \(U_R\) không đổi khi thay đổi \(R\) thì: \(Z_L=Z_C\), khi đó: \(U_R=U\)
\(\Rightarrow Z_C=Z_L=\omega.L=50\Omega\)
\(\dfrac{U.R}{\sqrt{R^2+\left(Z_L-Z_C\right)^2}}\) cho em hỏi đoạn này với ạ?