Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn:
\(U_{AB}=U_C=2\) (1)
\(U_{BC}^2=U_r^2+U_L^2=3\) (2)
\(U_{AC}^2=U_r^2+(U_L-U_C)^2=1\) (3)
Giải hệ 3 pt trên sẽ tìm đc \(U_r\) và \(U_L\)
Chia cho \(I\) sẽ tìm được \(r\) và \(Z_L\)

Từ ĐK đầu bài ta có:
tần số dao động riwwng của mạch là:
giải phương trình bâc 2 này ra ta được:

Khi tăng điện dung nên 2.5 lần thì dung kháng giảm 2.5 lần. Cường độ dòng trễ pha hơn hiệu điện thế $\pi/4$ nên
$Z_L-\frac{Z_C}{2.5}=R$
Trường hợp đầu tiên thì thay đổi C để hiệu điện thế trên C cực đại thì $Z_LZ_C=R^2+Z_L^2$
$Z_LZ_C=(Z_L-\frac{Z_C}{2.5})^2+Z_L^2$
Giải phương trình bậc 2 ta được: $Z_C=\frac{5}{4}Z_L$ hoặc $Z_C=10Z_L$(loại vì Zl-Zc/2.5=R<0)
$R=\frac{Z_L}{2}$
Vẽ giản đồ vecto ta được $U$ vuông góc với $U_{RL}$ còn $U_C$ ứng với cạch huyền
Góc hợp bởi U và I bằng với góc hợp bởi $U_L$ và $U_{LR}$
$\tan\alpha=\frac{R}{Z_L}=0.5$
$\sin\alpha=1/\sqrt5$
$U=U_C\sin\alpha=100V$
\(U_{C}{max}=\frac{U\sqrt{R^{2}+Z_L^{2}}}{R}\); \(Zc=\frac{R^{2}+Z_L^{2}}{Z_L}\)
khi C2=2,5C1---->Zc2=Zc1/2,5=ZC/2,5
do i trể pha hơn U nên Zl>Zc/2,5
\(\tan\frac{\pi }{4}=\frac{Z_L-0,4Zc}{R}=1\Rightarrow R=Z_L-0,4Z_C\)
\(\Rightarrow Z_C.Z_L=Z_L^{2}+(Z_L-0,4Z_C)^{2}\Rightarrow 2Z_L^{2}-1,8Z_CZ_L+0,16Z_C^{2}=0\Rightarrow Z_L=0,8Z_C;Z_L=0,1Z_C\)(loai)
\(\Rightarrow R=Z_L-1,25.0,4Z_L=0,5Z_L\)
\(\Rightarrow U_{C}{max}=\frac{U\sqrt{Z_L^{2}+0,25Z_L^{2}}}{0,5Z_L}=100\sqrt{5}\Rightarrow U=100V\)

Có: \(L=CR^2=Cr^2\Rightarrow R^2=r^2=Z_LZ_C,URC=\sqrt{3U}_{Lr}\Leftrightarrow Z^2_{RC}=3Z^2_{Lr}\Leftrightarrow R^2+Z^2_C=3\left(Z^2_L+R^2\right)\)
\(\Leftrightarrow-3Z^2_L+Z^2_C=2R^2\) (*) \(R^2=Z_LZ_C\) (**)
Từ (*) và (**) có: \(Z_L=\frac{R}{\sqrt{3}};Z_C=\sqrt{3}R\Rightarrow Z=\sqrt{\left(R+r\right)^2Z^2_{LC}}=\frac{4R}{\sqrt{3}}\Rightarrow\cos\phi=\frac{R+r}{Z}=\frac{\sqrt{3}}{2}\approx0,866\)
A đúng

Bạn nên gửi mỗi câu hỏi một bài thôi để mọi người tiện trao đổi.
1. \(Z_L=200\sqrt{3}\Omega\), \(Z_C=100\sqrt{3}\Omega\)
Suy ra biểu thức của i: \(i=1,1\sqrt{2}\cos\left(100\pi t-\frac{\pi}{3}\right)A\)
Công suất tức thời: p = u.i
Để điện áp sinh công dương thì p > 0, suy ra u và i cùng dấu.
Biểu diễn vị trí tương đối của u và i bằng véc tơ quay ta có:
u u i i 120° 120°
Như vậy, trong 1 chu kì, để u, i cùng dấu thì véc tơ u phải quét 2 góc như hình vẽ.
Tổng góc quét: 2.120 = 2400
Thời gian: \(t=\frac{240}{360}.T=\frac{2}{3}.\frac{2\pi}{100\pi}=\frac{1}{75}s\)
2. Khi nối tắt 2 đầu tụ điện thì cường độ dòng điện hiệu dụng không đổi \(\Rightarrow Z_1=Z_2\Leftrightarrow Z_C-Z_L=Z_L\Leftrightarrow Z_C=2Z_L\)
\(U_C=1,2U_d\Leftrightarrow Z_C=2Z_d\Leftrightarrow Z_C=2\sqrt{R^2+Z_L^2}\)
\(\Leftrightarrow2Z_L=\sqrt{R^2+Z_L^2}\Leftrightarrow R=\sqrt{3}Z_L\)
Khi bỏ tụ C thì cường độ dòng điện của mạch là: \(I=\frac{U}{Z_d}=\frac{U}{\sqrt{R^2+Z_L^2}}=\frac{220}{\sqrt{3.Z_L^2+Z_L^2}}=0,5\)
\(\Rightarrow Z_L=220\Omega\)

Bài này thì có vẹo gì đâu bạn.
\(u=100\sqrt 2\cos(100\pi t)(V)\)
\(Z_L=\omega L = 10\Omega\)
\(Z_C=\dfrac{1}{\omega C}=20\Omega\)
Tổng trở \(Z=\sqrt{r^2+(Z_L-Z_C)^2}=10\sqrt 2 \Omega\)
\(\Rightarrow I_o=\dfrac{U_0}{Z}=10A\)
\(\tan\varphi=\dfrac{Z_L-Z_C}{R}=-1\Rightarrow \varphi=-\dfrac{\pi}{4}\)
Suy ra: \(\varphi=\dfrac{\pi}{4}\)
Vậy \(i=10\cos(100\pi t +\dfrac{\pi}{4})\) (A)

Áp dụng công thức tính năng lượng điện từ trường ta có
W = Wđ = Wt \(\Rightarrow\frac{1}{2}LI_0^2=\frac{1}{2}lI^2+\frac{1}{2}Cu^2\)
\(\Rightarrow u=\sqrt{\left(I_0^2-I^2\right)\frac{L}{C}}\Rightarrow u=\)\(\sqrt{\frac{0,1}{10^{-5}}\left(0,05^2-0,02^2\right)}=4\left(V\right)\)
chọn A
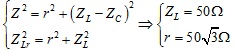
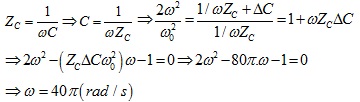
Đáp án D
Phương pháp: Sử dụng̣ vòng tròn lượng giác
Cách giải:
+ Trong quá trình dao động của mạch LC thì dòng điện luôn sớm pha π 3
so với điện áp hai đầu đoạn mạch
+ Phương pháp đường tròn
Từ hình vẽ ta thấy rằng sau khoảng thời gian T 3
điện áp giữa hai đầu tụ điện là - 3 2 U o và đang tăng