Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ChọnB.
Năng lượng ban đầu của tụ điện là W = 1 2 C U 2 = 5.10-3J = 5mJ. Khi dao động trong mạch tắt hẳn thì mạch không còn năng lượng. Năng lượng điện từ trong mạch đã bị mất mát hoàn toàn, tức là phần năng lượng bị mất mát là ΔW = 5mJ

Đáp án B
Phương pháp: Năng lượng mất đi đến khi tắt hẳn = Năng lượng ban đầu của hệ
Cách giải:
Năng lượng mất mát của mạch từ khi bắt đầu thực hiện dao động đến khi dao động điện từ tắt hẳn là
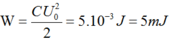

Khoảng thời gian liên tiếp giữa hai lần điện trường bằng năng lượng từ trường là \(\frac{T}{4}= \frac{\pi\sqrt{LC}}{2}.\).

\(T = 2\pi .\sqrt{LC} = 2.10^{-5}s.\)
Thời gian từ lúc hiệu điện thế trên tụ cực đại U0 đến lúc hiệu điện thế trên tụ \(+\frac{U_0}{2}\) tính dựa vào đường tròn
U 0 +U 0 2
\(\cos \varphi = \frac{U_)/2}{U_0}= \frac{1}{2}=> \varphi= \frac{\pi}{3}. \)
\( t = \frac{\varphi}{\omega}= \frac{\pi/3}{2\pi/T}= \frac{T}{6}= \frac{1}{3}.10^{-5}s.\)

Ta có: \(C_1=C_2=C_0\)
Mắc nối tiếp nên \(C_b=\dfrac{C_0}{2}\)
Ban đầu : \( W=\dfrac{C_bU_0^2}{2} ( \text{Với } U_0=8\sqrt{6}V)\)
Sau đó, đúng vào thời điểm dòng điện qua cuộn dây có giá trị bằng giá trị hiệu dụng thì \(W_t=W_đ=\dfrac{W}{2}\)
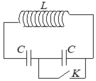
Đóng khoá K lại ta sẽ còn 1 tụ, và năng lượng điện giảm còn 1 nửa.
\(\Rightarrow W_{đ'}=\dfrac{W_đ}{2}=\dfrac{W}{4}\)
Khi đó: \(W'=W_t+W_{đ'}=\dfrac{C_0U_{02}^2}{2}\)
\(\Rightarrow U_{02}=12V\)

\(W= W_{Cmax}=W_C+W_L\)
=> \(W_L = W_{Cmax}-W_C= \frac{1}{2}C.(U_0^2-u^2)= 5.10^{-7}J.\)

Chọn A
Năng lượng ban đầu của mạch W0 = C U 0 2 2 2 = C U 0 2 4 = WC1 + WC2 + WL (Ở đây WC1 = WC2, do 2 tụ giống nhau) Vào lúc WC1 + WC2 = WL = W0/2, nối tắt một tụ (giả sử tụ C=2), năng lượng của mạch sau đó là: W = WC1 + WL = 3 4 W0 = 3 4 C U 0 2 4 = W' = C U ' 0 2 2 Do đó U 0 ' = U 0 3 8

Đáp án C
Phương pháp: Năng lượng điện từ trong mạch LC:
Cách giải:
Nhiệt lượng tỏa ra trong cuộn dây cho đến khi dao động tắt hẳn là: