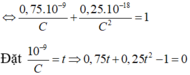Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(I_0 = q_0.\omega = 10^{-9}.10^4= 10^{-5}A.\)
\(\left(\frac{q}{q_0}\right)^2+\left(\frac{i}{I_0}\right)^2=1\)
=> \(\left(\frac{q}{q_0}\right)^2 = 1-\left(\frac{i}{I_0}\right)^2 = 1-\left(\frac{6.10^{-6}}{10^{-5}}\right)^2= \frac{16}{25} \)
=> \(q = q_0.\frac{4}{5} = 8.10^{-10}C.\)

Ta có : \(\frac{T_{W_{\text{đ}}}}{6}=1,5.10^{-4}\)
\(\Rightarrow\frac{T_q}{6}=\frac{2T_{W_{\text{đ}}}}{6}=3.10^{-4}\)
Vậy chọn D.

Ta có: \(W=W_t+W_d\)
\(\Leftrightarrow W_t=W_{dmax}-W_d\)
\(=\frac{1}{2}C.U^2_0-\frac{1}{2}Cu^2\)
\(=5.10^{-5}J\)

Sử sụng hệ thức: 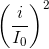 +
+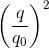 = 1
= 1
Thay số và giải hệ phương trình trìm I0 và q0
Tần số góc: ω = 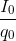 = 50 (rad/s)
= 50 (rad/s)

\(T = 2\pi .\sqrt{LC} = 2.10^{-5}s.\)
Thời gian từ lúc hiệu điện thế trên tụ cực đại U0 đến lúc hiệu điện thế trên tụ \(+\frac{U_0}{2}\) tính dựa vào đường tròn
U 0 +U 0 2
\(\cos \varphi = \frac{U_)/2}{U_0}= \frac{1}{2}=> \varphi= \frac{\pi}{3}. \)
\( t = \frac{\varphi}{\omega}= \frac{\pi/3}{2\pi/T}= \frac{T}{6}= \frac{1}{3}.10^{-5}s.\)

Hướng dẫn giải:
Thời gian để tụ phòng hết điện tích (q0 -> 0) được tính như sau
\(t = \frac{\varphi}{\omega}=\frac{\pi/2}{2\pi/T}=\frac{T}{4} \) => \(T = 4.2.10^{-6}= 8.10^{-6}s.\)
\(I_0 = q_0.\omega = 10^{-8}.\frac{2\pi}{8.10^{-6}}= 2,5.\pi.10^{-3} => I = \frac{I_0}{\sqrt{2}} \approx 5,55 mA.\)


Dựa vào giản đồ xét tam giác vuông OAB có
\(\sin60=\frac{Uc}{U_{ }AB}\Rightarrow U_C=100.\sin60=50\sqrt{3}V\Rightarrow Z_C=\frac{U_C}{I}=\frac{50\sqrt{3}}{0.5}=100\sqrt{3}\Omega\)
=> \(C=\frac{1}{Z_C.\omega}\)
\(\cos60=\frac{U_R}{U_{AB}}\Rightarrow U_R=50\Omega\Rightarrow R=\frac{U_R}{I}=100\Omega\)
2. Công suất trên mạch có biểu thức
\(P=I^2R=\frac{U^2}{R^2+\left(Z_L-Z_C\right)^2}.R\\=\frac{U^2}{R^{ }+\frac{\left(Z_L-Z_C\right)^2}{R}}\)
L thay đổi để P max <=> Mẫu Min => áp dụng bất đẳng thức cô-si cho hai số không âm=> \(R=\left|Z_L-Z_C\right|\)
=> \(R=100-40=60\Omega\)
=>