Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Năng lượng mạch dao động:
\(W=\dfrac{1}{2}CU^2\)
\(\Rightarrow U=\sqrt{\dfrac{2W}{C}}=\sqrt{\dfrac{2\cdot2,5\cdot10^{-4}}{5\cdot10^{-6}}}=10V\)
Chọn C

Đáp án A
Phương pháp: Viết phương trình cường độ dòng điện trong mạch.
Cách giải: Giả sử phương trình điện tích là:![]()
Phương trình cường độ dòng điện là: ![]()
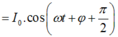 |

Tụ đang phóng điện tức là q đang giảm, ta có hình vẽ:
Vì q đang giảm nên I đang tăng và ta có phương trình của I là:
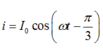
Với tần số góc:
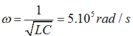
Khi năng lượng điện trường bằng một nửa năng lượng từ trường cực đại thì năng lượng từ trường cũng bằng một nửa năng lượng từ trường cực đại nên: 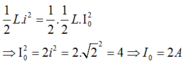
Vậy phương trình của dòng điện I là:
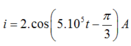

Chọn A
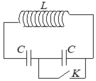
Năng lượng ban đầu của mạch W0 = C U 0 2 2 2 = C U 0 2 4 = WC1 + WC2 + WL (Ở đây WC1 = WC2, do 2 tụ giống nhau) Vào lúc WC1 + WC2 = WL = W0/2, nối tắt một tụ (giả sử tụ C=2), năng lượng của mạch sau đó là: W = WC1 + WL = 3 4 W0 = 3 4 C U 0 2 4 = W' = C U ' 0 2 2 Do đó U 0 ' = U 0 3 8

Áp dụng công thức tính năng lượng mạch dao động ta có
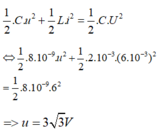
Đáp án D

Đáp án D
Phương pháp: Sử dụng công thức tính năng lượng mạch dao động và định luật bảo toàn năng lượng.
Cách giải: Áp dụng công thức tính năng lượng mạch dao động ta có:
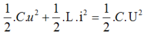
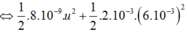
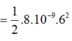
![]()

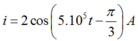
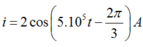
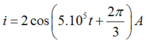
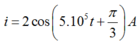
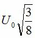
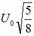
\(L=2mH=2\cdot10^{-3}H\)
\(I=4mA=4\cdot10^{-3}A\)
Năng lượng của mạch:
\(W=\dfrac{1}{2}L\cdot I^2=\dfrac{1}{2}\cdot2\cdot10^{-3}\cdot\left(4\cdot10^{-3}\right)^2=1,6\cdot10^{-8}J\)