Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài làm:
Ta có năng lượng từ trường cực đại bằng năng lượng điện trường cực đại:
$W_{tt max}=W_{đt max}=\dfrac{1}{2}.CU_o^2$
Từ đó ta có $C=10^{-8}(F)$

Bài này chỉ cần sử dụng công thức 2 giá trị của C để có cùng 1 giá trị của $U_C$ :
$U_C=U_{C_{max}} \cos \left(\dfrac{\varphi _1-\varphi _2}{2} \right)$
$\Rightarrow U_{C_{max}}=\dfrac{60}{\cos \dfrac{\pi }{6}}=40\sqrt{3} V$
Khi $U_{C_{max}}$ ta có:
$P=\dfrac{U^2}{R}\cos ^2\varphi _3=P_{max}\cos ^2\varphi _3=\dfrac{P_{max}}{2}$
$\Rightarrow \cos \varphi _3=\dfrac{\sqrt{2}}{2}$
Vẽ giản đồ suy ra: $U=\dfrac{U_{C_{max}}}{\sqrt{2}}=20\sqrt{6}\left(V \right)$

\(Z_L=\omega L=100\sqrt{3}\Omega\)
C thay đổi để Uc max khi: \(Z_C=\frac{R^2+Z_L^2}{Z_L}=\frac{100^2+3.100^2}{100\sqrt{3}}=\frac{4}{\sqrt{3}}.100\Omega\)
\(U_{cmax}=U\frac{\sqrt{R^2+Z_L^2}}{R}=100\frac{\sqrt{100^2+3.100^2}}{100}=200V\)

Điện áp ko đổi nhưng vẫn có dòng điện và dòng điện hữu hạn, chứng tỏ chỉ có 2 trường hợp:
1. Điện trở và cuộn cảm mắc nối tiếp (nối tiếp với tụ thì sẽ ko thể có dòng chạy qua)
2. Điện trở song song với tụ điện (nếu song song với cuộn cảm thuần thì sẽ bị chập mạch, tức là dòng lớn vô cùng)
Có thể bỏ qua trường hợp này vì điều kiện thứ 2.
Xét trường hợp 1:
Dễ dàng tính được: \(R=\frac{30}{2.5}=12\Omega\)
Mắc nối tiếp hộp kín với tụ điện C, ta có mạch RLC nối tiếp.
Theo bài ra, ta có hình vẽ: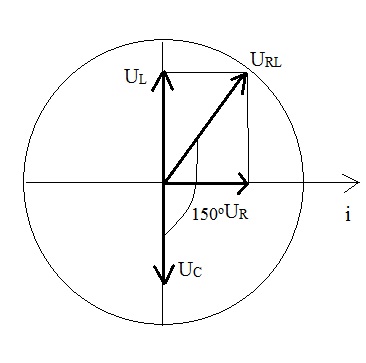
Từ hình vẽ ta có:
\(U_R=U_L\tan30^o\)
Suy ra:
\(Z_L=\frac{R}{\tan30^o}=12\sqrt{3}\Omega\)
Tổng trở của hộp kín:
\(Z=\sqrt{R^2+Z^2_L}=24\Omega\)

Tụ xoay có điện dung tỉ lệ với hàm số bậc nhất đối với góc xoay α => C = aα + b (a, b là hằng số)
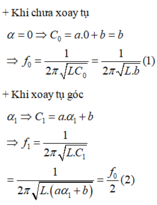
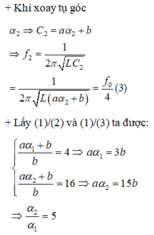
Đáp án D

Giải thích: Đáp án A
Phương pháp: Cường độ dòng điện hiệu dụng I = U/Z
Đoạn mạch gồm RLC mắc nối tiếp : 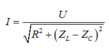 (1)
(1)
Khi nối tắt tụ : 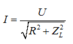
Từ (1) và (2)
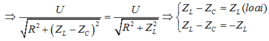
![]()


\(\lambda = c.2\pi\sqrt{LC}\)
\(\Rightarrow C = \dfrac{113^2}{(3.10^8)^2.40.20.10^{-6}}=1,8.10^{-10}F\)=180pF > 120 pF
Nên cần mắc thêm tụ C2 song song với C1 và có điện dung là: 180 - 120 = 60 pF
Chọn A.