Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lập hai pt độc lập với thời gian:
\(A^2=x_1^2+\left(\frac{v_1}{\omega}\right)^2\)
\(A^2=x_2^2+\left(\frac{v_2}{\omega}\right)^2\)
cho hai VP bằng nhau, giải pt được ω=20 (rad/s)
Thay vào 1 trong 2 pt đầu được A=6(cm)
Chúc bạn học tốt! :D

Theo công thức liên hệ chiều dài day và số bụng sóng ta có $2,4=8.\dfrac{\lambda}{2} \Rightarrow \lambda =0,6m=60 cm$
Công thức tính biên độ tại một điểm bất kì trên sợi dây cách nút gần nhất một khoảng là d đang có sóng dừng với biên độ tại bụng là 2A:
$a=2A \cos \left(\dfrac{2 \pi d}{\lambda} +\dfrac{\pi }{2} \right).$
Gọi khoảng cách từ A tới nút gần nhất là d thì do $\dfrac{\lambda}{4}<20$ nên ta có B cách nút gần nhất với nó một khoảng 10-d.
$| a_A-a_B |=2A |\left(\dfrac{2 \pi d}{\lambda} +\dfrac{\pi }{2} \right)-\left(\dfrac{2 \pi \left(10-d\right)}{\lambda} +\dfrac{\pi }{2} \right) |$
$=4A |\sin \left(\dfrac{10 \pi }{\lambda}+\dfrac{\pi }{2} \right) | |\sin \left(\dfrac{\pi \left(2x-10\right)}{\lambda}\right) |.$
Biểu thức trên lớn nhất khi $|\sin \left(\dfrac{\pi \left(2x-10\right)}{\lambda}\right) |$ lớn nhất, tức là bằng 1.
Thay số ta có đáp án D

Bài này chỉ cần sử dụng công thức 2 giá trị của C để có cùng 1 giá trị của $U_C$ :
$U_C=U_{C_{max}} \cos \left(\dfrac{\varphi _1-\varphi _2}{2} \right)$
$\Rightarrow U_{C_{max}}=\dfrac{60}{\cos \dfrac{\pi }{6}}=40\sqrt{3} V$
Khi $U_{C_{max}}$ ta có:
$P=\dfrac{U^2}{R}\cos ^2\varphi _3=P_{max}\cos ^2\varphi _3=\dfrac{P_{max}}{2}$
$\Rightarrow \cos \varphi _3=\dfrac{\sqrt{2}}{2}$
Vẽ giản đồ suy ra: $U=\dfrac{U_{C_{max}}}{\sqrt{2}}=20\sqrt{6}\left(V \right)$

Bạn áp dụng CT của dao động điều hòa:
\(A^2=x^2+\dfrac{v^2}{\omega^2}\)
Với \(x=\alpha.\ell\), li độ là độ dài cung của góc \(\alpha\) (tính theo rad)
\(\Rightarrow (\alpha_0.\ell)^2=(\alpha.\ell)^2+\dfrac{v^2.\ell}{g}\)
\(\Rightarrow \alpha_0^2=\alpha^2+\dfrac{v^2}{g\ell}\)
Chọn đáp án A.

Như ta biết, bản chất của giao thoa sóng là tổng hợp dao động do 2 nguồn truyền đến.
Do đó, dao động tại M là tổng hợp 2 dao động do A và B truyền đến.
Bước sóng: \(\lambda = 30/10 = 3cm\)
Độ lệch pha 2 dao động từ A, B truyền đến là: \(\Delta \varphi = 2\pi\frac{d_2-d_1}{\lambda}=2\pi\frac{13,5-10,5}{3}=2\pi\) (rad)
Biên độ tổng hợp: \(A_M=\sqrt{A_A^2+A_B^2+2A_AA_B\cos\Delta\varphi}=\sqrt{2^2+2^2+2.2.2.\cos2\pi}=4\)(cm)
Đáp án B

a 30
\(\omega =4\pi(rad/s)\)
\(|a|\le160\sqrt 3\) ứng với phần gạch đỏ trên hình, thời gian 1/3T ứng với véc tơ quay 1 góc 1200,.
Do vậy, mỗi một góc nhỏ là 300
\(\Rightarrow a_{max}=\dfrac{a}{\sin 30^0}=2a=320\sqrt 3(cm/s) \)
\(\Rightarrow A = \dfrac{a_{max}}{\omega^2}=2\sqrt 3(cm)\)
Cơ năng: \(W=\dfrac{1}{2}kA^2\Rightarrow k=\dfrac{2W}{A^2}=\dfrac{0,004}{(0,02\sqrt 3)^2}=...\)
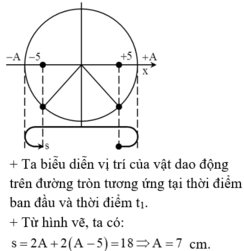

Chọn A
Lực kéo về F = -kx nên nó tỉ lệ với độ lớn li độ x và luôn hướng về vị trí cân bằng.