K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
PT
Pham Trong Bach
16 tháng 11 2018

Một lớp học có 40 học sinh trong đó có 15 học sinh giỏi Toán, 10 học sinh giỏi Văn và 5 học sinh giỏi cả Văn và Toán. Chọn ngẫu nhiên một học sinh.

a) Xác suất của biến cố A:”học sinh được chọn giỏi Toán” là:

A. 1/40

B. 8/3

C. 3/8

D. 1/8Ta có n(Ω) = 40
#Toán lớp 11
1
CM
Cao Minh Tâm
16 tháng 11 2018

Ta có n(Ω) = 40

a) Rõ ràng n(A) = 15 nên P(A) = 15/40 = 3/8

Chọn đáp án là C

Đúng(0)
PT
Pham Trong Bach
11 tháng 4 2019
Lớp 11A có 40 học sinh trong đó có 12 học sinh đạt điểm tổng kết môn Hóa học loại giỏi và 13 học sinh đạt điểm tổng kết môn Vật lí loại giỏi. Biết rằng khi chọn một học sinh của lớp đạt điểm tổng kết môn Hóa học hoặc Vật lí loại giỏi có xác suất là 0,5. Số học sinh đạt điểm tổng kết giỏi cả hai môn Hóa học và Vật lí là A.  4. B.  7. C.  6. D.  5....
Đọc tiếp

Lớp 11A có 40 học sinh trong đó có 12 học sinh đạt điểm tổng kết môn Hóa học loại giỏi và 13 học sinh đạt điểm tổng kết môn Vật lí loại giỏi. Biết rằng khi chọn một học sinh của lớp đạt điểm tổng kết môn Hóa học hoặc Vật lí loại giỏi có xác suất là 0,5. Số học sinh đạt điểm tổng kết giỏi cả hai môn Hóa học và Vật lí là

A.  4.

B.  7.

C.  6.

D.  5.
#Toán lớp 11
1
CM
Cao Minh Tâm
11 tháng 4 2019

Đáp án D

Gọi A là biến cố “Học sinh được chọn đạt điểm tổng kết loại giỏi môn Hóa học”.

B là biến cố “Học sinh được chọn đạt điểm tổng kết loại giỏi môn Vật lí”.

⇒ A C = a 3       A ∪ B  là biến cố “Học sinh được chọn đạt điểm tổng kết môn Hóa học hoặc Vật lí loại giỏi”.

A ∩ B  là biến cố “Học sinh được chọn đạt điểm tổng kết loại giỏi cả hai môn Hóa học và Vật lí”.

Đúng(0)
PT
Pham Trong Bach
18 tháng 12 2018

Một lớp học có 40 học sinh trong đó coa 15 học sinh giỏi Toán, 10 học sinh giỏi Văn và 5 học sinh giỏi cả Văn và Toán. Chọn ngẫu nhiên một học sinh.

c) Xác suất của biến cố C:”học sinh được chọn không giỏi Văn và Toán” là:

A. 15/32

B. 7/8

C. 1/2

D. Một đáp số khác
#Toán lớp 11
1
CM
Cao Minh Tâm
18 tháng 12 2018

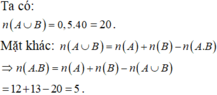
Ta có n(Ω) = 40

c) Nhận thấy :

Mà P(A∪B) = P(A) + P(B) –P(A∩B), A∩B là biến cố:”học sinh được chọn giỏi cả Văn và Toán” nên n(A∩B)=5/40=1/8

Chọn đáp án C

Nhận xét:

ở ý a) và b) học sinh có thể nhầm khi quan niệm: chọn 1 học sinh nên n(A) =n(B) =1 ⇒ phương án A; hoặc chọn 1 học sinh trong 5 học sinh giỏi Toán và Văn nên n(A) =n(B) = 5

⇒ P(A) =P(B) =5/40=1/8 (phương án D); hoặc sử dụng nhầm công thức P(A) =(n(Ω))/(n(A))=8/3;P(B)=(n(Ω))/(n(B))=4 (phương án C)

ở ý c), học sinh có thể nhầm khi quan niệm:

Nhưng  A ¯   v à   B ¯ không phải là hai biến cố độc lập

Có thể giải ý c) cách khác như sau:

Số học sinh giỏi Văn và Toán gồm: học sinh giỏi Văn, học sinh hioir Toán, học sinh giỏi cả Văn và Toán nên bằng (15 +10) -5 = 20 em. Do đó, số học sinh không giỏi cả Toán và Văn là 40 – 20 = 20 em, nên n(C) = 20

Vì vậy P(C) =(n(C))/(n(Ω))=1/2

Đúng(0)
PT
Pham Trong Bach
19 tháng 9 2018

Một lớp học có 40 học sinh trong đó coa 15 học sinh giỏi Toán, 10 học sinh giỏi Văn và 5 học sinh giỏi cả Văn và Toán. Chọn ngẫu nhiên một học sinh.

b) Xác suất của biến cố B:”học sinh được chọn giỏi Văn” là:

A. 1/40

B. 1/4

C. 4

D. 1/8
#Toán lớp 11
1
CM
Cao Minh Tâm
19 tháng 9 2018

Ta có n(Ω) = 40

b) Rõ ràng n(B) = 10 nên P(B) = 10/40 =1/4

Chọn đáp án B

Đúng(0)
NP
Nguyễn Phan Nhật Huy
3 tháng 12 2021

Lớp 11A1 có 12 học sinh giỏi,trong đó có 5 học sinh giỏi văn và 10 học sinh giỏi Toán. Chọn ngẫu nhiên 2 học sinh. Tính xác suất sao cho cả2 học sinh được chọn chỉgiỏi 1 môn.
#Toán lớp 11
1
DP
Đinh Phi Yến
3 tháng 12 2021

Có 2 bạn giỏi văn , 7 bạn giỏi toán, 3 bạn giỏi cả 2 môn

Có 2C1.7C1 =14 ( cách )

Đúng(0)
NT
nguyễn tuấn
27 tháng 4 2020 - olm
Câu 1Tính   A. 0B. 1 C. 2D. 3Câu 2Cho hình chóp S.ABC có SA vuông góc với (ABC) và tam giác ABC là tam giác vuông tại B. AH là đường cao của tam giác SAB. Phát biểu nào sau đây là sai?  A. B.  C. D. Câu 3Tính   A. Không tồn tạiB. C.  D. Câu 4Tính   A.  0B. 4 C. 9D. Câu 5Cho hình lập phương ABCD.A’B’C’D’. Khi đó góc giữa đường thẳng BC và B’D’ là:  A. B.  C. D. Câu...
Đọc tiếp

Câu 1

Tính 

 

 

A. 0

B. 1

 

C. 2

D. 3

Câu 2

Cho hình chóp S.ABC có SA vuông góc với (ABC) và tam giác ABC là tam giác vuông tại B. AH là đường cao của tam giác SAB. Phát biểu nào sau đây là sai?

 

 

A. 

B. 

 

C. 

D. 

Câu 3

Tính 

 

 

A. Không tồn tại

B. 

C. 

 

D. 

Câu 4

Tính 

 

 

A.  0

B. 4

 

C. 9

D. 

Câu 5

Cho hình lập phương ABCD.A’B’C’D’. Khi đó góc giữa đường thẳng BC và B’D’ là:

 

 

A. 

B. 

 

C. 

D. 

Câu 6

Tính .

 

 

A. 3

B. 

C. 

 

D. 2

Câu 7

Gọi  là VTCP của 2 đường thẳng d và d’. Nếu  thì:

 

 

A. 

B. 

 

C. 

D. 

Câu 8

Tính 

 

 

A. 

B. 

C. 

 

D. 

Câu 9

Có bao nhiêu đường thẳng đi qua 1 điểm và vuông góc với 1 mặt phẳng cho trước?

 

 

A. 0

B. 2

C. Vô số

 

D. 1

Câu 10

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O và SA = SC, SB = SD. Khi đó:

 

 

A. 

B. 

 

C. 

D. 

Câu 11

Cho . Khi đó  bằng:

 

 

A. 

B. 

C. 

 

D. 

Câu 12

Phát biểu nào sau đây là sai?

 

 

A. Một đường thẳng vuông góc với một mặt phẳng thì đường đường thẳng đó vuông góc với mọi đường thẳng nằm trong mặt phẳng.

B. Một đường thẳng vuông góc với một mặt phẳng nếu đường thẳng đó vuông góc với hai đường thẳng nằm trong mặt phẳng

C. Cho hai mặt phẳng song song với nhau, một đường thẳng vuông góc với mặt phẳng này thì cũng vuông góc với mặt phẳng còn lại.

 

D. Cho hai đường thẳng song song, một mặt phẳng vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng còn lại.

Câu 13

Cho ba đường thẳng phân biệt a, b, c. Phát biểu nào sau đây là sai?

 

 

A. 

B. 

C. 

 

D. 

Câu 14

Cho hình chóp S.ABC có SA vuông góc với (ABC) và tam giác ABC là tam giác vuông tại B. Vẽ AH là đường cao của tam giác SAB. Phát biểu nào sau đây là sai?

 

 

A. 

B. 

C. 

 

D. 

Câu 15

Cho hình chóp S.ABC với đáy ABC là tam giác đều và SA vuông góc với đáy. Gọi I là trung điểm BC. Mệnh đề nào sau đây là đúng?

 

 

A. 

B. 

C. 

 

D. 

Câu 16

Tính tổng 

 

 

A. 2

B. 

C. 

D. 4

 

Câu 17

Cho hình chóp S.ABCD với đáy ABCD là hình thoi tâm O và SA=SC. Khẳng định nào sau đây là đúng?

 

 

A. 

B. 

C. 

D. 

 

Câu 18

Tính 

 

 

A. Không tồn tại

B. 4

 

C. 

D. 

Câu 19

Tính 

 

 

A. 4

B. 

 

C. 0

D. Không tồn tại

Câu 20

Tính 

 

 

A. 3

B. 2

C. 0

 

D. 1

Câu 21

Cho . Tính 

 

 

A. 3

B. 2

C. 4

 

D. 1

Câu 22

Cho . Khi đó:

 

 

A. 

B. 

C. 

 

D. 

Câu 23

Cho hai đường thẳng phân biệt a, b và mặt phẳng (P). Mệnh đề nào sau đây là đúng?

 

 

A. 

B. 

C. 

 

D. 

Câu 24

Cho hình hộp ABCD.A’B’C’D’. Phát biểu nào sau đây là đúng?

 

 

A. 

B. 

C. 

 

D. 

Câu 25

Tính .

 

 

A. 

B. 0

 

C. 

D. 

Câu 26

Tính . Tìm b.

 

 

A. 1

B. 

 

C. 

D. 2

Câu 27

Tính .

 

 

A. 

B. 6

C. 0

D. 1

 

Câu 28

Cho hàm số . Tính .

 

 

A. Không tồn tại

B. 2

C. 

D. 1

 

Câu 29

Cho hình chóp S.ABCD với SA = SB = SC = SD và đáy là hình vuông tâm O. Vẽ  và . Khi đó:

 

 

A. 

B. 

C. 

D. 

 

Câu 30

Tính .

 

 

A. 

B. 

C. 

D. 2

 

Câu 31

Tính  với .

 

 

A. 

B. 

C. Không tồn tại

D. 0

 

Câu 32

Cho  và . Khi đó  bằng:

 

 

A. Không tồn tại

B. 

C. 

D. 0

 

Câu 33

Tính 

 

 

A. 0

 

B. Không tồn tại

C. 

D. 

Câu 34

Tính 

 

 

A. 

 

B. 3

C. 

D. 2

Câu 35

Cho . Khi đó  bằng:

 

 

A. 

 

B. 

C. 

D. 0

Câu 36

Tính 

 

 

A. 1

 

B. 0

C. 

D. 

Câu 37

Tính 

 

 

A. 

 

B. 1

C. 

D. 2

Câu 38

Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O và SA vuông góc với đáy. Phát biểu nào sau đây là sai?

 

 

A. 

 

B. 

C. 

D. 

Câu 39

Cho . Khi đó  bằng

 

 

A. 

 

B. 

C. Không tồn tại

D. 

Câu 40

Cho . Tính .

 

 

A. 2

 

B. 

C. 1

D. 
#Toán lớp 11
1
G
ღŤ.Ť.Đღ
27 tháng 4 2020

Bn nên xem lại cái đề

Đúng(0)
N
Nastu_Draneel
22 tháng 10 2016
1: tìm x , y , z :a, \(\frac{1}{2}x=\frac{2}{3}y=\frac{3}{4}z\) và \(x-y=15\)b, \(\frac{x}{2}=\frac{y}{3}\) ; \(\frac{y}{5}=\frac{z}{7}\) và \(x+y+z=92\)c, \(2x=3y=10z-2y-3y\) và \(x+y-z=95\)2 : cho \(\frac{a}{b}=\frac{c}{d}\left(a,b,c,d\ne0\right)\) và đôi 1 khác nhau , khác đôi nhau Chứng minh :a , \(\frac{a-b}{a+b}=\frac{c-d}{c+d}\)b ,...
Đọc tiếp

1: tìm x , y , z :

a, \(\frac{1}{2}x=\frac{2}{3}y=\frac{3}{4}z\) và \(x-y=15\)

b, \(\frac{x}{2}=\frac{y}{3}\) ; \(\frac{y}{5}=\frac{z}{7}\) và \(x+y+z=92\)

c, \(2x=3y=10z-2y-3y\) và \(x+y-z=95\)

2 : cho \(\frac{a}{b}=\frac{c}{d}\left(a,b,c,d\ne0\right)\) và đôi 1 khác nhau , khác đôi nhau

Chứng minh :

a , \(\frac{a-b}{a+b}=\frac{c-d}{c+d}\)

b , \(\frac{2a+5b}{3a-4b}=\frac{2c+5d}{3c-4d}\)

banhbanhquabatngobucminhbucquaeoeogianroiheheoekhocroi

 
#Toán lớp 11
2
CL
Cơ Liên Mỹ
18 tháng 9 2019

2 : cho ab=cd(a,b,c,d≠0)ab=cd(a,b,c,d≠0) và đôi 1 khác nhau, khác đôi nhau

Chứng minh :

a) C1: Đặt \(\frac{a}{b}=\frac{c}{d}=k\)\(\Rightarrow\left\{{}\begin{matrix}a=kb\\c=kd\end{matrix}\right.\)

\(\frac{a-b}{a+b}=\frac{kb-b}{kb+b}=\frac{b\left(k-1\right)}{b\left(k+1\right)}=\frac{k-1}{k+1}\)

\(\frac{c-d}{c+d}=\frac{kd-d}{kd+d}=\frac{d\left(k-1\right)}{d\left(k+1\right)}\frac{k-1}{k+1}\)

Đúng(0)
NL
Nguyễn Lê Phước Thịnh
5 tháng 2 2022

Bài 1: 

a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{2}=\dfrac{y}{\dfrac{3}{2}}=\dfrac{z}{\dfrac{4}{3}}=\dfrac{x-y}{2-\dfrac{3}{2}}=\dfrac{15}{\dfrac{1}{2}}=30\)

Do đó: x=60; y=45; z=40

b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}=\dfrac{x+y+z}{10+15+21}=\dfrac{92}{46}=2\)

Do đó: x=20; y=30; z=42

Đúng(0)
PT
Pham Trong Bach
22 tháng 7 2019
Đội dự tuyển học sinh giỏi giải toán trên máy tính cầm tay môn toán của trường phổ thông trung học Hoàng Quốc Việt có 4 học sinh nam khối 12, 2 học sinh nữ khối 12 và 2 học sinh nam khối 11. Để thành lập đội tuyển dự thi học sinh giỏi giải toán trên máy tính cầm tay môn toán cấp tỉnh nhà trường cần chọn 5 em từ 8 em học sinh trên. Tính xác suất để trong 5 em được chọn có cả học sinh...
Đọc tiếp

Đội dự tuyển học sinh giỏi giải toán trên máy tính cầm tay môn toán của trường phổ thông trung học Hoàng Quốc Việt có 4 học sinh nam khối 12, 2 học sinh nữ khối 12 và 2 học sinh nam khối 11. Để thành lập đội tuyển dự thi học sinh giỏi giải toán trên máy tính cầm tay môn toán cấp tỉnh nhà trường cần chọn 5 em từ 8 em học sinh trên. Tính xác suất để trong 5 em được chọn có cả học sinh nam và học sinh nữ, có cả học sinh khối 11 và học sinh khối 12?

A. LCCKPNI3dBW4.png

B. 2bgcOBcgCIaq.png

C. laMj8IvlWPmh.png

D. 4vxG6FEDLnGo.png
#Toán lớp 11
1
CM
Cao Minh Tâm
22 tháng 7 2019

Đáp án B.

Số cách chọn 5 em học sinh từ 8 học sinh trên là Piolyf5rhOyJ.pngcách

- Để chọn 5 em thỏa mãn bài ra, ta xét các trường hợp sau

+) 1 nam khối 11, 1 nữ khối 12 và 3 nam khối 12 có o1oifwZb9VIQ.pngcách

+) 1 nam khối 11, 2 nữ khối 12 và 2 nam khối 12 có SgWZQ31JqDHD.pngcách

+) 2 nam khối 11, 1 nữ khối 12 và 2 nam khối 12 có 4ym1QJo6EGo9.pngcách

+) 2 nam khối 11, 2 nữ khối 12 và 1 nam khối 12 có hTymGnNoQmH9.pngcách

- Số cách chọn 5 em thỏa mãn bài ra là:

ornUidD4BtVp.pngcách

Vậy xác suất cần tính là: mqepdKQ62mFx.png

Đúng(0)
PT
Phan Thị Ngọc Tú
14 tháng 9 2016

Giúp mình với khocroi 
Bạn nào giỏi phần tìm thiết diện của hình học không gian thì pm giúp mình với đi.
Please !!!!
#Toán lớp 11
0
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP