
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
Gọi chiều dài là x(Điều kiện: x>10,5)
Chiều rộng là 21-x
Theo đề, ta có: \(x^2+\left(21-x\right)^2=225\)
\(\Leftrightarrow x^2+x^2-42x+441-225=0\)
\(\Leftrightarrow2x^2-42x+216=0\)
\(\Leftrightarrow x^2-21x+108=0\)
\(\Leftrightarrow\left(x-12\right)\left(x-9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=12\left(nhận\right)\\x=9\left(loại\right)\end{matrix}\right.\)
vậy: Chiều dài là 12m
Chiều rộng là 9m


Bài 3:
a: Ta có: \(x-2\sqrt{x+8}=0\)
\(\Leftrightarrow\sqrt{4x+32}=x\)
\(\Leftrightarrow4x+32=x^2\)
\(\Leftrightarrow x^2-4x-32=0\)
\(\Leftrightarrow\left(x-8\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=8\left(nhận\right)\\x=-4\left(loại\right)\end{matrix}\right.\)
b: Ta có: \(3\sqrt{x+5}=4x-7\)
\(\Leftrightarrow\left(4x-7\right)^2=9x+45\)
\(\Leftrightarrow16x^2-56x+49-9x-45=0\)
\(\Leftrightarrow16x^2-65x+4=0\)
\(\Leftrightarrow16x^2-64x-x+4=0\)
\(\Leftrightarrow\left(x-4\right)\left(16x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=\dfrac{1}{16}\end{matrix}\right.\)

\(M=\sqrt{\dfrac{4}{\left(2-\sqrt{5}\right)^2}}-\sqrt{\dfrac{4}{\left(2+\sqrt{5}\right)^2}}=\dfrac{2}{\left|2-\sqrt{5}\right|}-\dfrac{2}{\left|2+\sqrt{5}\right|}\)
\(=\dfrac{2}{\sqrt{5}-2}-\dfrac{2}{\sqrt{5}+2}=\dfrac{2\left(\sqrt{5}+2\right)-2\left(\sqrt{5}-2\right)}{\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)}\)
\(=\dfrac{8}{1}=8\)
Lm ơn giúp mik đii mà mik bt ơn bn đó nhiều lắm . Mik đang rất cần

Lời giải:
a. Gọi biểu thức là $A$
\(A=\left[\frac{(1-\sqrt{x})(1+\sqrt{x}+x)}{1-\sqrt{x}}+\sqrt{x}\right].\left[\frac{1-\sqrt{x}}{(1-\sqrt{x})(1+\sqrt{x})}\right]^2\)
\(=(1+\sqrt{x}+x+\sqrt{x}).\frac{1}{(1+\sqrt{x})^2}=(\sqrt{x}+1)^2.\frac{1}{(\sqrt{x}+1)^2}=1\)
Ta có đpcm
b.
\(\sqrt{2012}-\sqrt{2011}=\frac{1}{\sqrt{2012}+\sqrt{2011}}< \frac{1}{\sqrt{2011}+\sqrt{2010}}=\sqrt{2011}-\sqrt{2010}\)

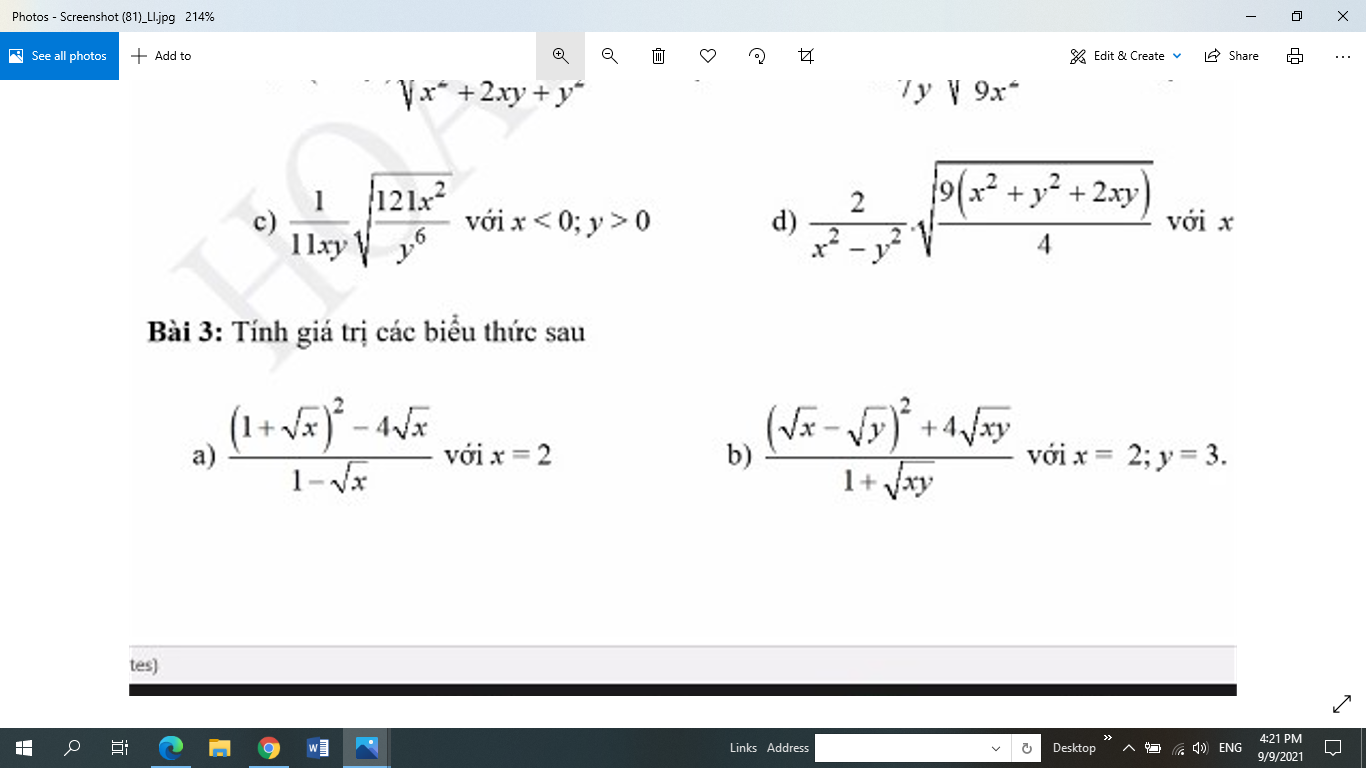
\(3,\\ a,\dfrac{\left(1+\sqrt{x}\right)^2-4\sqrt{x}}{1-\sqrt{x}}\\ =\dfrac{\sqrt{x}-2\sqrt{x}+1}{1-\sqrt{x}}=\dfrac{\left(1-\sqrt{x}\right)^2}{1-\sqrt{x}}=1-\sqrt{x}=1-\sqrt{2}\)
\(b,\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2+4\sqrt{xy}}{1+\sqrt{xy}}\\ =\dfrac{x+2\sqrt{xy}+y}{1+\sqrt{xy}}=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2}{1+\sqrt{xy}}\\ =\dfrac{\left(\sqrt{2}+\sqrt{3}\right)^2}{1+\sqrt{6}}=\dfrac{5+2\sqrt{6}}{1+\sqrt{6}}\\ =\dfrac{\left(5+2\sqrt{6}\right)\left(\sqrt{6}-1\right)}{5}\\ =\dfrac{3\sqrt{6}+7}{5}\)
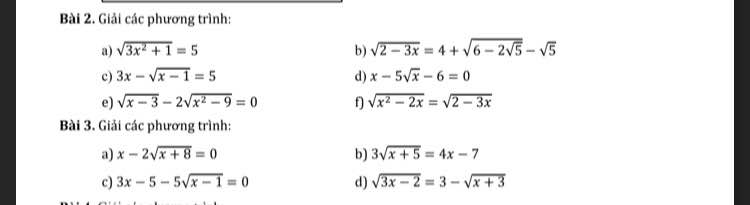


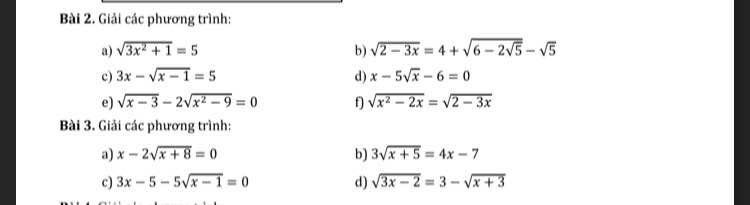


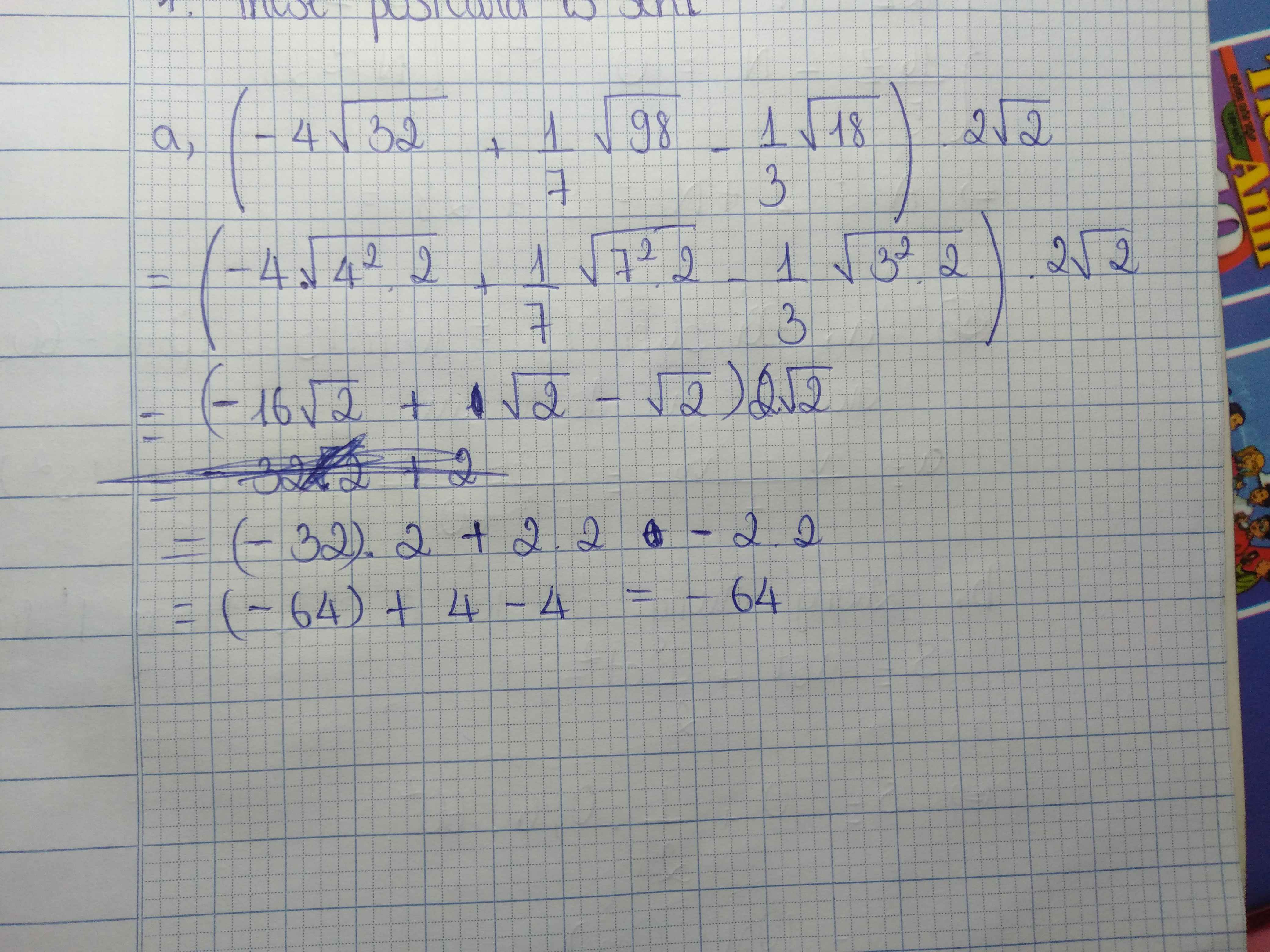


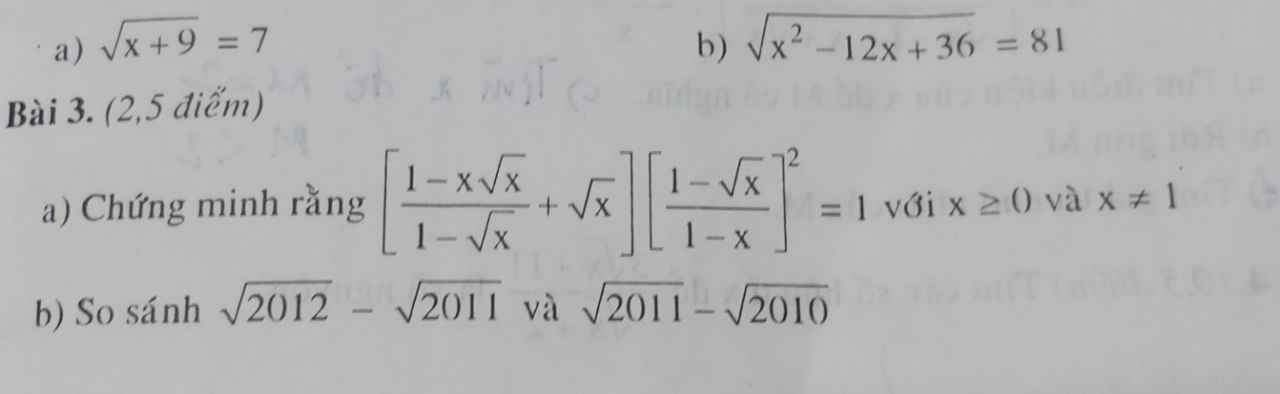
Bài 2:
c: Ta có: \(3x-\sqrt{x-1}=5\)
\(\Leftrightarrow\sqrt{x-1}=3x-5\)
\(\Leftrightarrow9x^2-30x+25-x+1=0\)
\(\Leftrightarrow9x^2-31x+26=0\)
\(\text{Δ}=\left(-31\right)^2-4\cdot9\cdot26=25\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{31-5}{18}=\dfrac{13}{9}\\x_2=\dfrac{31+5}{18}=2\end{matrix}\right.\)