
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A.(x+2y).(x+2y-1) = x^2 +4xy + 4y^2 - x - 2y
B. (x-2y).(x+2y-1) = x^2 - x - 4y^2 + 2y
C. (x-2y).(x-2y+1) = x^2 - 4xy + 4y^2 + x - 2y
D.(x+2y).(x-2y) = x^2 - 4y^2
=>....

1) \(\left(x+2y\right)^2=x^2+4xy+4y^2\)
2) \(\left(2x+3y\right)^2=4x^2+12xy+9y^2\)
3) \(\left(x+\frac{1}{3}\right)^4=\left[\left(x+\frac{1}{3}\right)^2\right]^2=\left(x^2+\frac{2}{3}x+\frac{1}{9}\right)^2=x^4+\frac{4}{9}x^2+\frac{1}{81}+\frac{4}{3}x^3+\frac{4}{27}x+\frac{2}{9}x^2=x^4+\frac{2}{3}x^2+\frac{1}{81}+\frac{4}{3}x^3+\frac{4}{27}x\)
4) \(\left(2x+y^2\right)^3=8x^3+12x^2y^2+6xy^4+y^6\)
5) Sửa đề: \(\left(\frac{x}{2}-2y\right)^3=\frac{x^3}{8}-\frac{3x^2}{2}+6xy^2-8y^3\)
6) \(\left(\sqrt{2x-y}\right)^4=\left(2x-y\right)^2=4x^2-4xy+y^2\)
7) \(\left(x+1\right)\left(x^2-x+1\right)=x^3+1\)
8) \(\left(x-3\right)\left(x^2+3x+9\right)=x^3-27\)

cau a : (3x^2y-6xy+9x)(-4/3xy)
=-4/3xy.3x^2y+4/3xy.6xy-4/3xy.9x
=-4x+8-8y
cau b : (1/3x+2y)(1/9x^2-2/3xy+4y^2)
=(1/3)^3-2/9x^2y+8y^3+4/3xy^2+2/9x^2y-4/3xy^2+8y^3
=(1/3)^3 + (2y)^3x-2
cau c : (x-2)(x^2-5x+1)+x(x^2+11)
=x^3-5x^2+x-2x^2+10x-2+x^3+11x
=2x^3-7x^2+22x-2
cau d := x^3 + 6xy^2 -27y^3
cau e := x^3 + 3x^2 -5x - 3x^2y - 9xy = 15y
cau f := x^2-2x+2x -4-2x-1
= x(x-2)-5

a)\(=\left(x^2-7x-9x+63\right)+1\)
\(=x^2-7x-9x+63+1\)
=\(x^2-16x+64\)
\(=\left(x-8\right)^2\)
a: \(=x^2-16x+63+1\)
\(=x^2-16x+64=\left(x-8\right)^2\)
b: \(=\left(x^2+x\right)^2-2\left(x^2+x\right)+1+4\left(x^2+x\right)\)
\(=\left(x^2+x\right)^2+2\left(x^2+x\right)+1\)
\(=\left(x^2+x+1\right)^2\)
c: \(=\left(x+2y-3-2\right)^2\)
\(=\left(x+2y-5\right)^2\)
d: \(=\left(x-y\right)^3-1-3\left(x-y\right)^2+3\left(x-y\right)\)
\(=\left(x-y-1\right)^3\)

a) \(-2x\left(10x-3\right)+5x\left(4x+1\right)=25\)
\(-20x^2+6x+20x^2+5x=25\)
\(\Rightarrow6x+5x=25\)
\(\Rightarrow11x=25\)
\(\Rightarrow x=\dfrac{25}{11}\)
b) \(y\left(5-2y\right)+2y\left(y-1\right)=15\)
\(5y-2y^2+2y^2-2y=15\)
\(\Rightarrow5y-2y=15\)
\(\Rightarrow3y=15\)
\(\Rightarrow y=5\)
c)\(x\left(x+1\right)-\left(x+1\right)=35\)
\(\Rightarrow\left(x-1\right)\left(x+1\right)=35\)
\(\Rightarrow x^2-1=35\)
\(\Rightarrow x^2=36\)
\(\Rightarrow x=6;x=-6\)
d)\(x\left(x^2+x+1\right)-x^2\left(x+1\right)=0\)
\(x^3+x^2+x-x^3+x=0\)
\(\Rightarrow x^2+2x=0\)
\(\Rightarrow x\left(x+2\right)=0\)
\(\Rightarrow x=0;x=0-2=-2\)
Vậy \(x=0;x=-2\)

a)\((\dfrac{5}{7}x^2y)^3:(\dfrac{1}{7}xy)^3\)
=\((\dfrac{5}{7}x^2y:\dfrac{1}{7}:x:y)^3\)
=(\(\dfrac{5}{7}.7.x^2:x.y:y)^3\)
=(5x)\(^3\)
=5\(^3\).x\(^3\)
=125.x\(^3\)

\(B=\left[\left(\frac{x}{y}-\frac{y}{x}\right):\left(x-y\right)-2.\left(\frac{1}{y}-\frac{1}{x}\right)\right]:\frac{x-y}{y}\)
\(=\left[\frac{x^2-y^2}{xy}.\frac{1}{x-y}-2.\frac{x-y}{xy}\right].\frac{y}{x-y}\)
\(=\left(\frac{\left(x-y\right)\left(x+y\right)}{xy.\left(x-y\right)}-\frac{2.\left(x-y\right)}{xy}\right).\frac{y}{x-y}\)
\(=\left(\frac{x+y}{xy}-\frac{2x-2y}{xy}\right).\frac{y}{x-y}=\frac{x+y-2x+2y}{xy}.\frac{y}{x-y}=\frac{y.\left(3y-x\right)}{xy.\left(x-y\right)}=\frac{3y-x}{x.\left(x-y\right)}\)
\(C=\left(\frac{x+y}{2x-2y}-\frac{x-y}{2x+2y}-\frac{2y^2}{y-x}\right):\frac{2y}{x-y}\)
\(=\left(\frac{x+y}{2.\left(x-y\right)}-\frac{x-y}{2.\left(x+y\right)}+\frac{2y^2}{x-y}\right).\frac{x-y}{2y}\)
\(=\frac{\left(x+y\right)^2-\left(x-y\right)^2+2.2y^2.\left(x+y\right)}{2.\left(x-y\right)\left(x+y\right)}.\frac{x-y}{2y}\)
\(=\frac{\left(x+y+x-y\right)\left(x+y-x+y\right)+4y^2.\left(x+y\right)}{2.\left(x-y\right)\left(x+y\right)}.\frac{x-y}{2y}\)
\(=\frac{4xy+4xy^2+4y^3}{2.\left(x-y\right)\left(x+y\right)}.\frac{x-y}{2y}=\frac{4y.\left(x+xy+y^2\right).\left(x-y\right)}{4y.\left(x-y\right)\left(x+y\right)}=\frac{x+xy+y^2}{x+y}\)
\(D=3x:\left\{\frac{x^2-y^2}{x^3+y^3}.\left[\left(x-\frac{x^2+y^2}{y}\right):\left(\frac{1}{x}-\frac{1}{y}\right)\right]\right\}\)
\(=3x:\left\{\frac{\left(x+y\right)\left(x-y\right)}{\left(x+y\right)\left(x^2-xy+y^2\right)}.\left[\frac{xy-x^2-y^2}{y}:\frac{y-x}{xy}\right]\right\}\)
\(=3x:\left[\frac{x-y}{x^2-xy+y^2}.\left(\frac{xy-x^2-y^2}{y}.\frac{xy}{y-x}\right)\right]\)
\(=3x:\left(\frac{x-y}{x^2-xy+y^2}.\frac{xy.\left(x^2-xy+y^2\right)}{y.\left(x-y\right)}\right)\)
\(=3x:\frac{xy.\left(x-y\right)\left(x^2-xy+y^2\right)}{y.\left(x-y\right)\left(x^2-xy+y^2\right)}=3x:x=3\)
\(E=\frac{2}{x.\left(x+1\right)}+\frac{2}{\left(x+1\right)\left(x+2\right)}+\frac{2}{\left(x+2\right)\left(x+3\right)}\)
\(=2.\left(\frac{1}{x.\left(x+1\right)}+\frac{1}{\left(x+1\right)\left(x+2\right)}+\frac{1}{\left(x+2\right)\left(x+3\right)}\right)\)
\(=2.\frac{\left(x+2\right)\left(x+3\right)+x.\left(x+3\right)+x.\left(x+1\right)}{x.\left(x+1\right)\left(x+2\right)\left(x+3\right)}\)
\(=2.\frac{x^2+2x+3x+6+x^2+3x+x^2+x}{x.\left(x+1\right)\left(x+2\right)\left(x+3\right)}\)
\(=2.\frac{3x^2+9x+6}{x.\left(x+1\right)\left(x+2\right)\left(x+3\right)}=2.\frac{3.\left(x^2+3x+2\right)}{x.\left(x+1\right)\left(x+2\right)\left(x+3\right)}\)
\(=\frac{6.\left(x^2+x+2x+2\right)}{x.\left(x+1\right)\left(x+2\right)\left(x+3\right)}=\frac{6.\left[x.\left(x+1\right)+2.\left(x+1\right)\right]}{x.\left(x+1\right)\left(x+2\right)\left(x+3\right)}\)
\(=\frac{6.\left(x+1\right)\left(x+2\right)}{x.\left(x+1\right)\left(x+2\right)\left(x+3\right)}=\frac{6}{x.\left(x+3\right)}\)
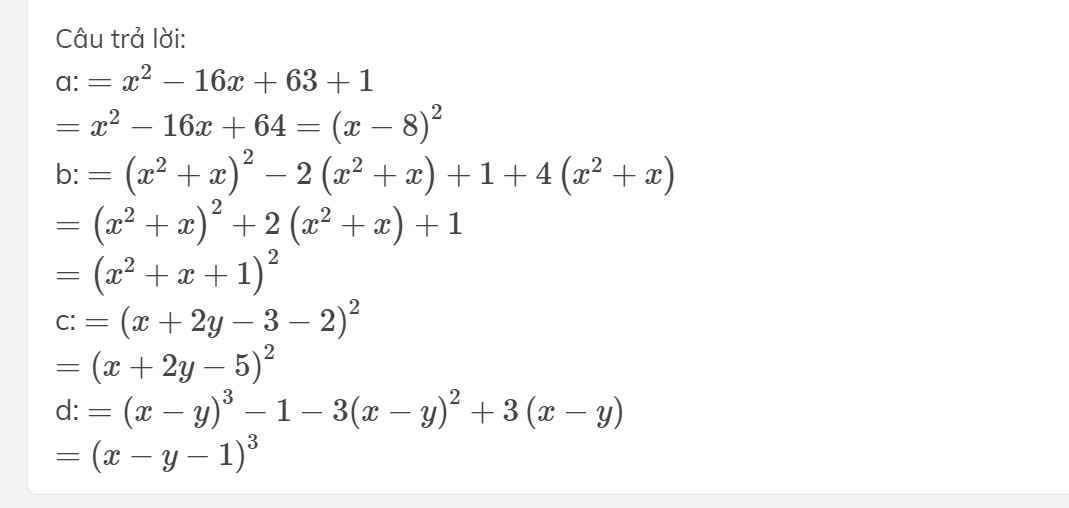
\(-\left(x-1\right)\left(-x^2+2y\right)\)
\(=\left(x-1\right)\left(x^2-2y\right)\)
\(=x^3-2xy-x^2+2y\)
\(-(x-1)(-x^2+2y)\)
\(=-\left\lbrack x(-x^2+2y)-1(-x^2+2y)\right\rbrack\)
\(=-\left\lbrack-x^3+2xy+x^2-2y\right\rbrack\)
\(=x^3-x^2-2xy+2y\)