
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





Lời giải:
Áp dụng công thức tính góc giữa hai đường thẳng thôi:
\(\cos (d,\Delta)=\frac{|(m+3)(m-2)-(m-1)(m+1)|}{\sqrt{(m+3)^2+(m-1)^2}\sqrt{(m-2)^2+(m+1)^2}}=\cos 90=0\)
\(\Leftrightarrow (m+3)(m-2)-(m-1)(m+1)=0\)
\(\Leftrightarrow m-5=0\Leftrightarrow m=5\)
Vậy $m=5$

Lời giải:
Áp dụng BĐT Bunhiacopxky:
\(\left (\frac{1}{a}+\frac{1}{b}\right)(a+b)\geq (1+1)^2\Rightarrow \frac{1}{a}+\frac{1}{b}\geq \frac{4}{a+b}\) (đpcm)
Áp dụng công thức trên (cho tất cả các phần)
a) \(\left\{\begin{matrix} \frac{1}{a}+\frac{1}{b}\geq \frac{4}{a+b}\\ \frac{1}{b}+\frac{1}{c}\geq \frac{4}{b+c}\\ \frac{1}{c}+\frac{1}{a}\geq \frac{4}{a+c}\end{matrix}\right.\) \(\Rightarrow \) cộng theo về, rút gọn: \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\geq \frac{2}{a+b}+\frac{2}{b+c}+\frac{2}{c+a}\)
Ta có đpcm.
b) Áp dụng CT: \(\left\{\begin{matrix} \frac{1}{a+b}+\frac{1}{a+c}\geq \frac{4}{a+b+a+c}=\frac{4}{2a+b+c}\\ \frac{1}{b+c}+\frac{1}{a+c}\geq \frac{4}{a+b+2c}\\ \frac{1}{a+b}+\frac{1}{b+c}\geq \frac{4}{a+2b+c}\end{matrix}\right.\)
Cộng theo vế và rút gọn:
\(\Rightarrow \frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}\geq 2\left (\frac{1}{a+2b+c}+\frac{1}{2a+b+c}+\frac{1}{a+b+2c}\right)\)
Ta có đpcm.
c) Áp dụng hai phần a và b:
\(\text{VP}\leq \frac{1}{2}\left (\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}\right)\leq \frac{1}{4}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)
\(\Leftrightarrow \text{VP}\leq \frac{4}{4}=1\) (đpcm)
Dấu bằng xảy ra ở tất cả các phần đều là khi \(a=b=c\)

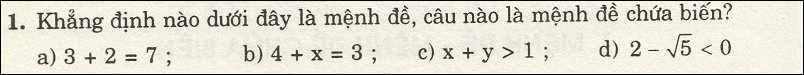

 . Tìm m để góc giữa hai đường thẳng đó
. Tìm m để góc giữa hai đường thẳng đó  , với:
, với:
 . Áp dụng chứng minh các BĐT sau:
. Áp dụng chứng minh các BĐT sau:




