Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

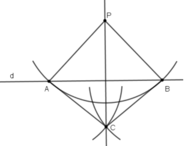
a) Ta có: PA = PB (A; B nằm trên cung tròn tâm P) nên P nằm trên đường trung trực của AB.
CA = CB (C nằm trên 2 cung tròn tâm A, B bán kính bằng nhau) nên C nằm trên đường trung trực của AB.
Vậy CP là đường trung trực của AB, suy ra PC ⊥ d.
b) Một cách vẽ khác
- Lấy hai điểm A, B bất kì trên d.
- Vẽ cung tròn tâm A bán kính AP, cung tròn tâm B bán kính BP. Hai cung tròn cắt nhau tại C (C khác P).
- Vẽ đường thẳng PC. Khi đó PC là đường đi qua P và vuông góc với d.
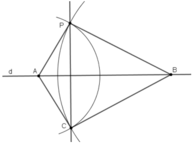
Chứng minh :
- Theo định lí 2 :
PA = CA ( P,C cùng thuộc cung tròn tâm A bán kính PA)
⇒ A thuộc đường trung trực của PC.
PB = CB (P, C cùng thuộc cung tròn tâm B bán kính PB)
⇒ B thuộc đường trung trực của PC.
⇒ AB là đường trung trực của PC
⇒ PC ⏊ AB hay PC ⏊ d.

- Duy nhất chỉ có một
- Nếu có nhiều đường thẳng thì các đường thẳng đó trùng nhau

1: Qua một điểm nằm ngoài đường thẳng, có một và chỉ một đường thẳng đi qua điểm đó và vuông góc với đường thẳng cho trước
có duy nhất 1 đường thẳng qua một điểm và vuông góc với đường thẳng cho trước