Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta tìm bán kính R2 = IM2 => R2 = IM = (2 + 2)2 + (-3 -32) = 52
Phương trình đường tròn (C): (x +2)2 + (y – 3)2 =52
b) Đường tròn tiếp xúc với đường thẳng d nên khoảng cách từ tâm I tới đường thẳng d phải bằng bán kính đường tròn:
d(I; d) = R
Ta có : R = d(I; d) = \(=\)
Phương trình đường tròn cần tìm là:
(x +1)2 + (y – 2)2 = =>( x +1)2 + (y – 2)2 =
<=> 5x2 + 5y2 +10x – 20y +21 = 0
c) Tâm I là trung điểm của AB, có tọa độ :
x = \(\dfrac{1+7}{2}\) = 4; y = \(\dfrac{1+5}{2}\) = 3 => I(4; 3)
AB = \(2\sqrt{13}\) => R =\(\sqrt{13}\)
=> (x -4 )2 + (y – 3)2 =13

Đường tròn tâm O(a,b)
\(\Delta_1\) đi qua \(AB..\Delta_1:\left(x-1\right)-\left(y-2\right)=x-y+1=0\)
\(\Delta_2\) trung trực AB: \(\Delta_2:\left(x-2\right)+\left(y-3\right)=x+y-5=0\)
Tâm (c) phải thuộc \(\Delta_2\) =>O(a,5-a)
Gọi I là điểm tiếp xúc \(\Delta\) và (C) ta có hệ pt
\(\Rightarrow\left\{{}\begin{matrix}OA=OB=\sqrt{\left(a-1\right)^2+\left(5-a-3\right)^2}=R\\OI=\left|3a+\left(5-a\right)-3\right|=\sqrt{10}R\end{matrix}\right.\)
\(\left\{{}\begin{matrix}a^2-2a+1+a^2-4a+4=R^2\\\left(2a+2\right)^2=10R^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2a^2-6a+5=R^2\\4a^2+8a+4=10R^2\end{matrix}\right.\)
Lấy [(1) nhân 5] trừ [(2) chia 2]
\(\Leftrightarrow8a^2-32a+23=0\left\{\Delta=16^2-8.23=8.32-8.23=8\left(32-23\right)=2.4.9\right\}\) đề số lẻ thế nhỉ
\(\Rightarrow a=\left[{}\begin{matrix}\dfrac{16-6\sqrt{2}}{8}=2-\dfrac{3\sqrt{2}}{4}\\\dfrac{16+6\sqrt{2}}{8}=2+\dfrac{3\sqrt{2}}{4}\end{matrix}\right.\)
\(\Rightarrow b=\left[{}\begin{matrix}3+\dfrac{3\sqrt{2}}{4}\\3-\dfrac{3\sqrt{2}}{4}\end{matrix}\right.\) \(\Rightarrow R^2=\left[{}\begin{matrix}\dfrac{\left(6-\dfrac{3\sqrt{2}}{2}\right)^2}{10}\\\dfrac{\left(6+\dfrac{3\sqrt{2}}{2}\right)^2}{10}\end{matrix}\right.\)
(C) =(x-2+3sqrt(2)/4)^2 +(y-3-3sqrt(2)/4)^2 =(6-3sqrt(2)/2)^2/10

a) \(\left\{{}\begin{matrix}x=-5+4t\\y=-2-3t\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}x=\sqrt{3}+2t\\y=1+3t\end{matrix}\right.\)

pt đường thẳng (AB)d: (x+1)-3(y-2)=x-3y+7=0
đường thẳng (d1) qua M// AB => d1//d
đảm bảo yêu cầu đầu bài
d1: (x-2)-3(x-5)=x-3y+13=0
Có hai trường hợp:
Th1. d đi qua \(M\left(2;5\right)\) và song song với đường thẳng AB.
Một vtcp\(\overrightarrow{v_d}=\overrightarrow{AB}\left(6;2\right)=2\left(3;1\right)\).
Phương trình đường thẳng d là: \(3\left(x-2\right)+1\left(y-5\right)=0\)\(\Leftrightarrow3x+y-11=0\).
Th2. d đi qua \(M\left(2;5\right)\) và trung điểm của AB.
Gọi I là trung điểm của AB.
\(x_I=\dfrac{-1+5}{2}=2;y_I=\dfrac{4+2}{2}=3\).
Vậy \(I\left(2;3\right)\).
Một véc tơ chỉ phương của d là: \(\overrightarrow{MI}=\left(0;-2\right)\).
Phương trình đường thẳng d là: \(0\left(x-2\right)-2\left(y-5\right)=0\)\(\Leftrightarrow y=5\).

a,\(\Delta_a\) : 3 (x-1) - 2 (y-1) =3x-2y-1=0
b, \(\Delta_b\) : y=-\(\dfrac{1}{2}\)(x-2) =-\(\dfrac{1}{2}\)x =>\(\Delta_b\) : x+2y=0
c,\(\overrightarrow{AB}\)=(-2;-3) =>vtpt \(\overrightarrow{n}\)=(3;-2)
=>\(\Delta_c\): 3 (x-2) - 2(y-0) =0
=>\(\Delta_c\): 3x-2y-6=0
Lời giải
a) \(\Delta_a=3\left(x-1\right)-2\left(y-1\right)=3x-2y+5=0\)
b)\(\Delta_b:y=-\dfrac{1}{2}\left(x-2\right)-1=-\dfrac{1}{2}x\Rightarrow\Delta_b:x+2y=0\)
c) \(\Delta_c:\left(3+0\right)\left(x-2\right)+\left(0-2\right)\left(y-0\right)=3x-2y-6\)

a) Thay x, y trong phương trình y = ax + b bằng tọa độ của A và của B ta được hệ phương trình:
Vậy phương trình của đường thẳng đi qua A(0; 3) và là: y = - 5x + 3.
b) Thay \(x,y\) trong phương trình \(y=ax+b\) bằng tọa độ A và B ta được hệ phương trình: \(\left\{{}\begin{matrix}1.a+b=2\\2.a+b=1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=-1\\b=3\end{matrix}\right.\).
Vậy phương trình đường thẳng cần tìm là: \(y=-x+3\).
c) Thay \(x,y\) trong phương trình \(y=ax+b\) bằng tọa độ A và B ta được hệ phương trình: \(\left\{{}\begin{matrix}15a+b=-3\\21a+b=-3\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=0\\b=-3\end{matrix}\right.\).
Vậy phương trình đường thẳng cần tìm là: \(y=-3\).

Các đường thẳng đều có phương trình dạng \(y=ax+b\). Các đường thẳng song song với nhau đều có cùng một hệ số a. Do đó các phương trình của các đường thẳng song song với đường thẳng \(y=3x-2\) đều có hệ số \(a=3\)
a) Phương trình cần tìm có dạng \(y=3x+b\). Vì đường thẳng đi qua điểm \(M\left(2;3\right)\), nên ta có \(3=3.2+b\Leftrightarrow b=-3\)
Vậy phương trình của đường thẳng đó là \(y=3x-3\)
b) \(y=3x+5\)


a) Sử dụng phương trình đường tròn : x2 - y2 - ax – 2by +c = 0
Đường tròn đi qua điểm A(1; 2):
12 + 22 – 2a -4b + c = 0 <=> 2a + 4b – c = 5
Đường tròn đi qua điểm B(5; 2):
52 + 22 – 10a -4b + c = 0 <=> 10a + 4b – c = 29
Đường tròn đi qua điểm C(1; -3):
12 + (-3)2 – 2a + 6b + c = 0 <=> 2a - 6b – c = 10
Để tìm a, b, c ta giải hệ: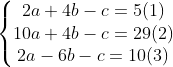
Lấy (2) trừ cho (1) ta được phương trình: 8a = 24 => a = 3
Lấy (3) trừ cho (1) ta được phương trình: -10b = 5 => b = - 0,5
Thế a = 3 ; b = -0.5 vào (1) ta tính được c = -1
Ta được phương trình đường tròn đi qua ba điểm A, B, C là :
x2 + y2 - 6x + y - 1 = 0.
b) Tương tự ta tính được I(2; 1), R= 5
Phương trình đường tròn đi qua ba điểm M(-2; 4); N(5; 5); P(6; -2) là:
(x - 2)2 + (y – 1)2 = 25 <=> x2 - y2 - 4x – 2y - 20 = 0