

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Vậy \(S=4\pi r^2=4\pi\left(\dfrac{a\sqrt{2}}{2}\right)^2=2\pi a^2\) và \(V=\dfrac{4}{3}\pi r^3=\dfrac{4}{3}\pi\left(\dfrac{a\sqrt{2}}{2}\right)^3=\dfrac{1}{3}\pi a^3\sqrt{2}\)

Gọi giao điểm của (α) với ba tia Ox, Oy, Oz lần lượt là A(a; 0; 0), B(0; b; 0), C(0; 0 ; c) (a, b, c > 0).
Mặt phẳng (α) có phương trình theo đoạn chắn là:
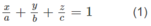
Do (α) đi qua M(1; 2; 3) nên ta thay tọa độ của điểm M vào (1):
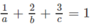
Thể tích của tứ diện OABC là:
![]()
Áp dụng bất đẳng thức Cô-si ta có:
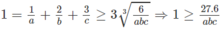
⇒ abc ≥ 27.6 ⇒ V ≥ 27
Ta có: V đạt giá trị nhỏ nhất ⇔ V = 27
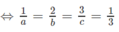
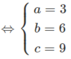
Vậy phương trình mặt phẳng ( α ) thỏa mãn đề bài là:
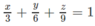
hay 6x + 3y + 2z – 18 = 0


a) Gọi H là hình chiếu vuông góc của tâm O trên mặt phẳng \(\left(\alpha\right)\).
Theo giả thiết ta có \(\widehat{OAH}=30^0\)
Do đó : \(HA=OA\cos30^0=r\dfrac{\sqrt{3}}{2}\)


a) Phương trình đường thẳng d có dạng: , với t ∈ R.
b) Đường thẳng d vuông góc với mặt phẳng (α): x + y - z + 5 = 0 nên có vectơ chỉ phương
(1 ; 1 ; -1) vì
là vectơ pháp tuyến của (α).
Do vậy phương trình tham số của d có dạng:
c) Vectơ (2 ; 3 ; 4) là vectơ chỉ phương của ∆. Vì d // ∆ nên
cùng là vectơ chỉ phương của d. Phương trình tham số của d có dạng:
d) Đường thẳng d đi qua hai điểm P(1 ; 2 ; 3) và Q(5 ; 4 ; 4) có vectơ chỉ phương
(4 ; 2 ; -1) nên phương trình tham số có dạng: