Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mệnh đề phủ định của P: P− “ π không là một số hữu tỉ”.
P là mệnh đề sai, P− là mệnh đề đúng.
Mệnh đề phủ định của Q: Q− “Tổng hai cạnh của một tam giác nhỏ hơn hoặc bằng cạnh thứ ba”.
Q là mệnh đề đúng, Q− là mệnh đề sai.

Mệnh đề “√2 là số hữu tỉ’’ sai vì √2 là số vô tỉ
Mệnh đề phủ định: "√2 không phải là một số hữu tỉ"

+) Mệnh đề phủ định của mệnh đề A là \(\overline A \): “Đồ thị hàm số y = x không là một đường thẳng”
Mệnh đề \(\overline A \) sai vì đồ thị hàm số y = x là một đường thẳng.
+) Mệnh đề phủ định của mệnh đề B là \(\overline B \): “Đồ thị hàm số \(y = {x^2}\) đi qua điểm A (3; 9)”
Mệnh đề \(\overline B \) đúng vì \(9 = {3^2}\) nên A (3;9) thuộc đồ thị hàm số \(y = {x^2}\).

a) \(\overline A \): “\(\frac{5}{{1,2}}\) không là một phân số”.
Đúng vì \(\frac{5}{{1,2}}\) không là phân số (do 1,2 không là số nguyên)
b) \(\overline B \): “Phương trình \({x^2} + 3x + 2 = 0\) vô nghiệm”.
Sai vì phương trình \({x^2} + 3x + 2 = 0\) có hai nghiệm là \(x = - 1\) và \(x = - 2\).
c) \(\overline C \): “\({2^2} + {2^3} \ne {2^{2 + 3}}\)”.
Đúng vì \({2^2} + {2^3} = 12 \ne 32 = {2^{2 + 3}}\).
d) \(\overline D \): “Số 2 025 không chia hết cho 15”.
Sai vì 2025 = 15. 135, chia hết cho 15.

Mệnh đề phủ định của các mệnh đề trên là:
a) “Paris không phải là thủ đô của nước Anh”
b) “23 không phải là số nguyên tố”
c) “2021 không chia hết cho 3”
d) “Phương trình \({x^2} - 3x + 4 = 0\) có nghiệm”.
+) Xét tính đúng sai:
a) “Paris là thủ đô của nước Anh” là mệnh đề sai.
“Paris không phải là thủ đô của nước Anh” là mệnh đề đúng.
b) “23 là số nguyên tố” là mệnh đề đúng.
“23 không phải là số nguyên tố” là mệnh đề sai.
c) “2021 chia hết cho 3” là mệnh đề sai.
“2021 không chia hết cho 3” là mệnh đề đúng.
d) “Phương trình \({x^2} - 3x + 4 = 0\) vô nghiệm” là mệnh đề đúng.
“Phương trình \({x^2} - 3x + 4 = 0\) có nghiệm” là mệnh đề sai.

Có ít nhất một hình vuông không phải là hình thoi. Mệnh đề sai.
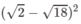
+) Mệnh đề phủ định của mệnh đề P là \(\overline P \): “5,15 không phải là một số hữu tỉ”
Mệnh đề P đúng, \(\overline P \) sai vì \(5,15 = \frac{{103}}{{20}} \in \mathbb{Q}\), là một số hữu tỉ.
+) Mệnh đề phủ định của mệnh đề Q là \(\overline Q \): “2 023 không phải là số chẵn” (hoặc “2 023 là số lẻ”)
Mệnh đề Q sai, \(\overline Q \) đúng vì 2 023 có chữ số tận cùng là \(3 \ne \left\{ {0;2;4;6;8} \right\}\), đo đó 2 023 không phải là số chẵn.
P: đúng
phủ định: "5,15 không phải số hữu tỉ"
Q: sai
Phủ định: "1023 không phải số chẵn"