Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B E C D 1 1
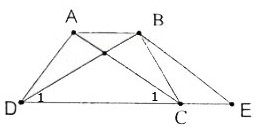
a) Hình thang ABEC ( AB // CE ) có hai cạnh bên AC, BE song song nên chúng bằng nhau: AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó \(\Delta BDE\)cân
b) Do AC // BE nên \(\widehat{E}=\widehat{C_1}\left(3\right)\)
Mà tam giác BDE cân tại B ( câu a ) nên \(\widehat{E}=\widehat{D_1}\left(4\right)\)
Từ (3)(4) => \(\widehat{D_1}=\widehat{C_1}\)
* Xét 2 tam giác : ACD và BDC có :
DC chung
AC = BD ( gt )
\(\widehat{C_1}=\widehat{D_1}\left(cmt\right)\)
\(\Rightarrow\Delta ACD=\Delta BDC\left(c-g-c\right)\)
c) Theo ( c/m câu b ) ta có :
\(\Delta ACD=\Delta BDC\)
nên \(\widehat{ADC}=\widehat{BCD}\)( 2 góc tương ứng )
Vậy hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.

a) Ta có :
P là trung điểm AB
Q là trung điểm AC
⇒⇒ PQ là đường trung bình tam giác ABC
Xét tứ giác BPQC , ta có :
PQ//BC( do PQ là đường trung bình tam giác ABC)
⇒⇒BPQC là hình thang (dấu hiệu nhận biết hình thang)
b)Ta có :
Q là trung điểm PE
Q là trung điểm AC
⇒⇒ Q là trung điểm hai đường chéo của tứ giác AECP
Suy ra tứ giác AECP là hình bình hành
a) Ta có :
P là trung điểm AB
Q là trung điểm AC
⇒ PQ là đường trung bình tam giác ABC
Xét tứ giác BPQC , ta có :
PQ//BC( do PQ là đường trung bình tam giác ABC)
⇒BPQC là hình thang (dấu hiệu nhận biết hình thang)

a) Hình thang ABEC (AB // CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau:
AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó tam giác BDE cân.
b) Ta có AC // BE suy ra  =
=  (3)
(3)
∆BDE cân tại B (câu a) nên  =
=  (4)
(4)
Từ (3) và (4) suy ra  =
= 
Xét ∆ACD và ∆BCD có AC = BD (gt)
 =
=  (cmt)
(cmt)
CD cạnh chung
Nên ∆ACD = ∆BDC (c.g.c)
c) ∆ACD = ∆BDC (câu b)
Suy ra 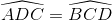
Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
Bài giải:
a) Hình thang ABEC (AB // CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau:

AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó tam giác BDE cân.
b) Ta có AC // BE suy ra  =
=  (3)
(3)
∆BDE cân tại B (câu a) nên  =
=  (4)
(4)
Từ (3) và (4) suy ra  =
= 
Xét ∆ACD và ∆BCD có AC = BD (gt)
 =
=  (cmt)
(cmt)
CD cạnh chung
Nên ∆ACD = ∆BDC (c.g.c)
c) ∆ACD = ∆BDC (câu b)
Suy ra 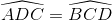
Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.

a/vì AB//DC(gt) suy ra AB//DE
và AC//BE(gt)
do hai đoạn thẳng song song(AB//DE) chắn bởi 2 đường thẳng song song (AC//BE) suy ra AC=BE
Mà AC=BD(gt)
suy ra BD=BE
Trong tam giác BDE có BD=BE suy ra tam giác BDE cân tại B (dpcm)
b/Chứng minh:tg ACD=tg BDC
VÌ tg BDE cân tại B nên ta có :GÓc B1 = GÓc E1(*)
Vì AC//BE(gt)
E=C1 là 2 góc đồng vị
suy ra góc C1 =góc E(**)
từ (*);(**) suy ra B1=C1
bạn tự xét tg nha
suy ra tg ACD=tg BDC
c/bạn tự cm lun nha

a) Vì tam giác ABC vuông tại A
=> BAC = 90 độ
=> Vì K là hình chiếu của H trên AB
=> HK vuông góc với AB
=> HKA = 90 độ
=> HKA = BAC = 90 độ
=> KH // AI
=> KHIA là hình thang
Mà I là hình chiếu của H trên AC
=> HIA = 90 độ
=> HIA = BAC = 90 độ
=> KHIA là hình thang cân
b) Vì KHIA là hình thang cân
=> KA = HI
= >KI = HA
Xét tam giác KAI vuông tại A và tam giác HIC vuông tại I có
KA = HI
KI = AH
=> Tam giác KAI = tam giác HIC ( cgv-ch)
=> KIA = ACB ( DPCM)
c) con ý này tớ nội dung chưa học đến thông cảm