
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\left(x^2+x+1\right)\left(x^2+x+2\right)-12\)
Đặt: \(x^2+x+1=y\), khi đó biểu thức trở thành:
\(y\left(y+1\right)-12\)
\(=y^2+y-12\)
\(=y^2-3y+4y-12\)
\(=y\left(y-3\right)+4\left(y-3\right)\)
\(=\left(y-3\right)\left(y+4\right)\)
\(=\left(x^2+x+1-3\right)\left(x^2+x+1+4\right)\)
\(=\left(x^2+x-2\right)\left(x^2+x+5\right)\)
\(=\left(x^2-x+2x-2\right)\left(x^2+x+5\right)\)
\(=\left[x\left(x-1\right)+2\left(x-1\right)\right]\left(x^2+x+5\right)\)
\(=\left(x-1\right)\left(x+2\right)\left(x^2+x+5\right)\)
b) \(\left(x^2+2x\right)^2+9x^2+18x+20\)
\(=\left(x^2+2x\right)^2+9\left(x^2+2x\right)+20\)
Đặt: \(x^2+2x=a\), khi đó biểu thức trở thành:
\(a^2+9a+20\)
\(=a^2+4a+5a+20\)
\(=a\left(a+4\right)+5\left(a+4\right)\)
\(=\left(a+4\right)\left(a+5\right)\)
\(=\left(x^2+2x+4\right)\left(x^2+2x+5\right)\)
c) \(\left(x+2\right)\left(x+4\right)\left(x+6\right)\left(x+8\right)+16\)
\(=\left[\left(x+2\right)\left(x+8\right)\right]\left[\left(x+4\right)\left(x+6\right)\right]+16\)
\(=\left(x^2+10x+16\right)\left(x^2+10x+24\right)+16\)
Đặt: \(x^2+10x+20=y\), khi đó biểu thức trở thành:
\(\left(y-4\right)\left(y+4\right)+16\)
\(=y^2-16+16\)
\(=y^2\)
\(=\left(x^2+10x+20\right)^2\)
$\text{#}Toru$

Gọi chiều rộng là x
Chiều dài là x+15
Theo đề, ta có phương trình:
\(\left(x+5\right)\left(x+12\right)=x\left(x+15\right)+80\)
\(\Leftrightarrow x^2+17x+60-x^2-15x=80\)
=>2x+60=80
=>x=10
Vậy: Chiều rộng là 10m
Chiều dài là 25m

Gọi độ dài quãng đường là x
Theo đề, ta có:
\(\dfrac{x}{42}-\dfrac{x}{46}=\dfrac{3}{4}\)
hay x=362,25(km)

\(3x-15=2x\left(x-5\right)\\ \Leftrightarrow3x-15=2x^2-10x\\ \Leftrightarrow3x+2x^2+10x=15\\ \Leftrightarrow13x+2x^2=15\\ \Leftrightarrow x\left(13+2x\right)=15\\ \Leftrightarrow\left[{}\begin{matrix}x=15\\2x=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=15\\x=1\end{matrix}\right.\)

b: ĐKXĐ: x>=2/3
PT=>(x-1)(x-2)+(x-1)*căn 3x-2=0
=>căn 3x-2+x-2=0
=>căn 3x-2=-x+2
=>x<=2 và 3x-2=x^2-4x+4
=>x^2-4x+4-3x+2=0 và x<=2
=>x=1
c: =>x+3+x-4-2căn (x^2-x-12)=1
=>2*căn x^2-x-12=2x-1-1=2x-2
=>căn x^2-x-12=x-1
=>x>=1 và x^2-x-12=x^2-2x+1
=>x=13

40: Ta có: \(A=27x^3+8y^3-3x-2y\)
\(=\left(3x+2y\right)\left(9x^2-6xy+4y^2\right)-\left(3x+2y\right)\)
\(=\left(3x+2y\right)\left(9x^2-6xy+4y^2-1\right)\)

\(P=x^2-2x+5=x^2-2x+1+4=\left(x-1\right)^2+4\)
Vì \(\left(x-1\right)^2\ge0\Rightarrow\left(x-1\right)^2+4\ge4\)
=>Pmin=(x-1)2+4=4
<=>(x-1)2=0
<=>x-1=0
<=>x=1
Vậy Pmin=4 khi x=1
----------------------------------------------------------
\(Q=2x^2-6x=2\left(x^2-3x\right)=2\left[x^2-2.x.\frac{3}{2}+\left(\frac{3}{2}\right)^2\right]-\frac{9}{2}=2\left(x-\frac{3}{2}\right)^2-\frac{9}{2}\)
Vì \(\left(x-\frac{3}{2}\right)^2\ge0\Rightarrow2\left(x-\frac{3}{2}\right)^2\ge0\Rightarrow2\left(x-\frac{3}{2}\right)^2-\frac{9}{2}\ge-\frac{9}{2}\)
=>Qmin=\(2\left(x-\frac{3}{2}\right)^2-\frac{9}{2}=-\frac{9}{2}\)
<=>\(2\left(x-\frac{3}{2}\right)^2=0\)
<=>\(\left(x-\frac{3}{2}\right)^2=0\)
<=>\(x-\frac{3}{2}=0\)
<=>\(x=\frac{3}{2}\)
Vậy Qmin=\(-\frac{9}{2}\) khi \(x=\frac{3}{2}\)

a: Xét ΔMQP có
H,I lần lượt là trung điểm của MQ,MP
=>HI là đường trung bình của ΔMQP
=>HI//QP và HI=QP/2
Xét ΔPMN có
I,K lần lượt là trung điểm của PM,PN
=>IK là đường trung bình của ΔPMN
=>IK//MN và \(IK=\dfrac{MN}{2}\)
b: H,I,K thẳng hàng
mà HI//PQ và IK//MN
nên HI//MN
Ta có: HI//MN
HI//PQ
Do đó: MN//PQ

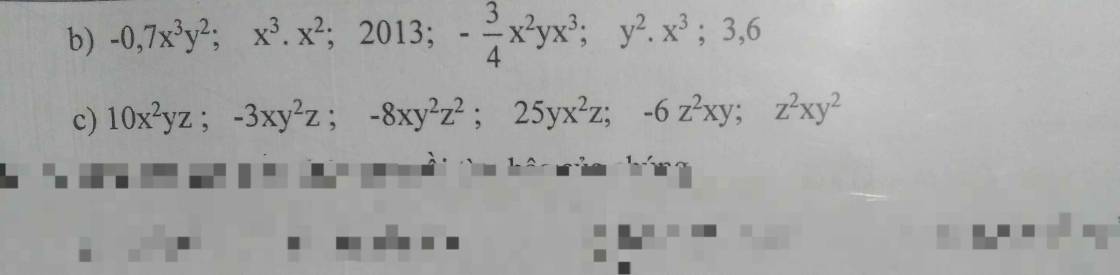
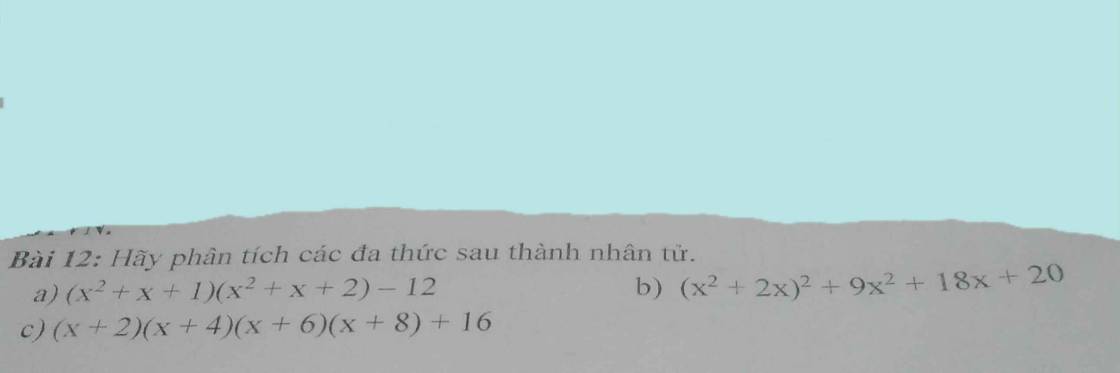





 Giải chi tiết 2 bài với ạ. Cần gấp. Cảm ơn ạ.
Giải chi tiết 2 bài với ạ. Cần gấp. Cảm ơn ạ.

2:
a: Các đơn thức đồng dạng là \(2.5xy^3;-2xy^3\)
b: Các đơn thức đồng dạng là \(2013;3,6\)
\(-0.7x^3y^2;y^2\cdot x^3\)
c: Các đơn thức đồng dạng là \(10x^2yz;25yx^2z\)
\(-8xy^2z^2;z^2xy^2\)
a) Các đơn thức đồng dạng là:
\(2,5xy^3\) và \(-2xy^3\)
b) Các đơn thức của đồng dạng:
\(-0,7x^3y^2\) và \(y^2\cdot x^3\)
\(3,6\) và \(2013\)
c) Các đơn thứ đồng dạng là:
\(-8xy^2z^2\) và \(z^2xy^2\)
\(10x^2yz\) và \(25yx^2z\)