Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi giá tiền quyển vở là \(x\)(\(x\in N\)*)
Gọi giá tiền cây viết là \(y\)(\(y\in N\)*)
Vì bạn Binh mua một quyển vở và một cây viết hết 12000 đồng,nên ta có : \(x+y=12000\left(1\right)\)
Do bạn Binh mua một quyển vở và một cây viết hết 12000 đồng, biết giá tiền của một quyển vở gấp đôi giá tiền của một cây viết, nên ta có : \(x=2y\) \(\Leftrightarrow x-2y=0\left(2\right)\)
Từ \(\left(1\right)\left(2\right)\) ta có hpt :
\(\left\{{}\begin{matrix}x+y=12000\\x-2y=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y-x+2y=12000\\x+y=12000\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3y=12000\\x+y=12000\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=4000\\x+y=12000\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=4000\\x+4000=12000\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=4000\left(n\right)\\x=8000\left(n\right)\end{matrix}\right.\)
Vậy giá tiền quyển vở là \(8000\left(đ\right)\)
giá tiền cây viết là \(4000\left(đ\right)\)

Gọi số tiền 1 quyển tập lúc chưa giảm giá là x (nghìn đồng) (x>0).(x>0).
Gọi số tiền 1 cây viết lúc chưa giảm giá là y (nghìn đồng) (y>0).(y>0).
Lúc đầu, An dự định mua 30 quyển tập và 10 cây viết hết 340 nghìn đồng nên ta có phương trình:
30x+10y=340(1)
Số tiền mua 1 quyển tập sau khi được giảm giá 10%10% là: x−x.10%=90%x(nghìn đồng)
Số tiền mua 1 cây viết sau được khi giảm 5%5% là: y−y.5%=95%y (nghìn đồng).
An mua 50 quyển tập và 20 cây viết với giá đã được giảm hết 526 nghìn đồng nên ta có phương trình:
50.90%x+20.95%y=526⇔45x+19y=526(2)
Từ (1) và (2) ta có hệ phương trình:
{30x+10y=34045x+19y=526⇔{3x+y=3445x+19y=526⇔{45x+15y=51045x+19y=526⇔{4y=163x+y=34⇔{y=43x+4=34⇔{x=10(tm)y=4(tm)
Vậy giá tiền mỗi quyển tập lúc chưa giảm giá là 10 nghìn đồng, mỗi cây viết lúc chưa giảm giá là 4 nghìn đồng.
Gọi số tiền 1 quyển tập lúc chưa giảm giá là x ( nghìn đồng ) ( x > 0 ).
Gọi số tiền 1 cây viết lúc chưa giảm giá là y ( nghìn đồng ) ( y> 0 ).
Lúc đầu, An dự định mua 30 quyển tập và 10 cây viết hết 340 nghìn đồng nên ta có phương trình:
30x + 10y = 340 (1)
Số tiền mua 1 quyển tập sau khi được giảm giá 10% là :
x - x . 10% = 90%x ( nghìn đồng )
Số tiền mua 1 cây viết sau được khi giảm 5% là :
y - y . 5% = 95%y ( nghìn đồng )
An mua 50 quyển tập và 20 cây viết với giá đã được giảm hết 526 nghìn đồng nên ta có phương trình:
50 . 90%x + 20 . 95%y = 526
⇔ 45x + 19y = 526 (2)
Từ (1) và (2) ta có hệ phương trình:
{30x+10y=34045x+19y=526{30x+10y=34045x+19y=526 ⇔ {3x+y=3445x+19y=526{3x+y=3445x+19y=526 ⇔ {45x+15y=51045x+19y=526{45x+15y=51045x+19y=526 ⇔ {4y=163x+y=34{4y=163x+y=34 ⇔ {y=43x+x=34{y=43x+x=34 {x=10(tm)y=4(tm){x=10(tm)y=4(tm)
Vậy giá tiền mỗi quyển tập lúc chưa giảm giá là 10 nghìn đồng, mỗi cây viết lúc chưa giảm giá là 4 nghìn đồng.

Gọi giá tiền của bàn ủi khi chưa khuyến mãi là x, ta có:
Giá tiền bàn ủi khi khuyến mãi:
\(\text{x−0,1x=0,9x }\)(đồng)
Giá tiền bộ lau nhà khi khuyến mãi:
\(\text{300000−0,9x}\) (đồng)
Giá tiền bộ lau nhà khi chưa khuyến mãi:
\(\text{(300000−0,9x).100:80=375000−1,125x}\) (đồng)
Vì tổng số tiền bàn ủi và bộ lau nhà khi chưa khuyến mãi là 350000 đồng nên:
\(\text{x+375000−1,125x=350000}\)
\(\text{↔0,125x=25000}\)
\(\text{↔x=200000}\)
\(\text{→375000−1,125.x=150000}\)
Vậy giá tiền của bàn ủi khi chưa khuyến mãi là \(\text{200000}\) đồng, giá tiền bộ lau nhà khi chưa khuyến mãi là \(\text{150000}\) đồng.

Chia 9 đồng tiền ra 3 phần bằng nhau, mỗi phần 3 đồng tiền. Để dễ thực hiện gọi ba nhóm lần lượt là nhóm A. nhóm B, nhóm C. đầu tiên ta cân nhóm A và nhóm B (Lần cân thứ nhất) . kia.
Trường hợp 1:
Nhóm A và nhóm B có một nhóm có khối lượng lớn hơn. Lúc này, ta lấy nhóm nặng hơn đó chia làm ba nhóm nhỏ hơn, mỗi nhóm một đồng, đặt hai đồng lên hai dĩa cân (Lần cân thứ hai). Nếu hai đồng này bằng nhau thì đồng thứ ba chính là đồng khác biệt, nếu hai đồng trên hai dĩa cân đồng nặng đồng nhẹ thì đồng nặng chính là đồng khác biệt.
Trường hợp 2:
Nhóm A và nhóm B bằng nhau. Nhóm C có đồng tiền khác biệt. Ta thực hiện như trường hơp 1, chia nhóm C làm ba phần, mỗi phân 1 đồng, đặt hai đồng lên hai bên dĩa cân rồi cân. ( Lần cân thứ hai).
Lưu ý: hai trường hợp này sẽ chỉ xảy ra một trường hợp.

Nửa chu vi tấm sắt là 96 : 2 = 48 (cm)
Gọi chiều dài của tấm sắt là x (cm) (x > 20)
Chiều rộng của tấm sắt sẽ là 48 – x (cm)
Diện tích của tấm sắt ban đầu là x (48 – x) ( c m 2 )
Người ta cắt ở mỗi góc tấm sắt một hình vuông cạnh là 4cm nên diện tích phần cắt đi là: 4.4.4 = 64 ( c m 2 )
Diện tích còn lại của tấm sắt là 448 c m 2 nên ta có phương trình:
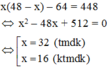
Vậy chiều dài và chiều rộng của tấm sắt lần lượt là 32cm và 16cm
Đáp án: A

Gọi x (đồng) là giá tiền một quả quýt và y (đồng) là giá tiền một quả cam. Điều kiện
x > 0, y > 0 ta có hệ phương trình:
<=> <=>
<=> .
Trả lời: Giá tiền một quả quýt: 800 đồng, một quả cam 1400 đồng
Chúc bạn học tốt!

C1:
Gọi số tiền niêm yết ban đầu của 1 cái bàn ủi là x (đồng)(x>0)
số tiền niêm yết ban đầu của 1 cái quạt điện là y (đồng)(y>0)
Vì anh Tường mua 1 cái bàn ủi và 1 cái quạt điện với tổng số tiền niêm yết là 850 000 nên ta có phương trình: x + y = 850 000 (1)
Số tiền được giảm của bàn ủi là: 10%x = 0,1x (đồng)
Số tiền được giảm của quạt điện là: 20%y = 0,2y (đồng)
Vì sau khi giảm giá anh Tường phải trả ít hơn 125 000 đồng nên ta có phương trình: 0,1x + 0,2y = 125000 (2)
Từ (1) và (2) ta có hệ phương trình:\(\hept{\begin{cases}x+y=850000\\0,1x+0,2y=125000\end{cases}}\)
Giải hệ ta có: x = 450000 y=400000
Vậy số tiền niêm yết của cái bàn ủi là 450000 đồng; số tiền niêm yết của quạt điên là 400000 đồng
Số tiền thực tế anh Tường phải trả cho 1 cái bàn ủi là: 450000 - 0,1 . 450000= 405000 (đồng)
Số tiền thực tế anh Tường phải trả cho 1 cái quạt điện là 400000- 0,2.400000= 320000 (đồng)

Gọi x (đồng) là giá tiền của 1kg sắt φ 8, y (đồng) là khoản chi phí làm trần của tầng một. Điều kiện: x > 0, y > 0
Khi đó giá tiền của 1kg sắt là φ 18 là 22x (đồng)
Vì tầng một dùng 30 cây sắt φ 18 và 350kg sắt φ 8 hết y đồng nên ta có: 30.22x + 350x = y
Vì tầng hai dùng 20 cây sắt φ 18 và 250kg sắt φ 8 hết ít hơn tầng một 1440000 đồng nên ta có: 20.22x + 250x = y – 1440000
Ta có hệ phương trình:
Giá trị của x và y thỏa điều kiện bài toán.
Vậy giá 1kg sắt φ 8 là 4500 đồng,
giá 1 cây sắt φ 18 là 4500.22 = 99000 đồng.
gooodddddddddddd