
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

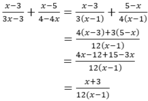

ĐK: x#0; x#-1
\(\frac{x^4}{1-x}\)+ x3 + x2 + 1
= \(\frac{x^4}{1-x}\)+ \(\frac{x^3\left(1-x\right)}{1-x}\)+ \(\frac{x^2\left(1-x\right)}{1-x}\)+ \(\frac{1-x}{1-x}\)
= \(\frac{x^4+x^3-x^4+x^2-x^3+1-x}{1-x}\)
= \(\frac{x+1}{1-x}\)

Câu 4: Không có nghĩa khi x-3=0
=>x=3
Câu 5:
\(A=\dfrac{x-3}{\left(x-3\right)\left(x+3\right)}=\dfrac{1}{x+3}\)

a,$\frac{5}{2x^2y}+\frac{3}{5xy^2}+\frac{x}{y^3}$52x2y +35xy2 +xy3
b,\(\frac{x+1}{2x+6}+\frac{2x+3}{x\left(x+3\right)}\)
Cộng vào sẽ ra kết quả nha !!!

\(x^5+x^4+x^3+x^2+x+1\)
\(=\left(x^5+x^4+x^3\right)+\left(x^2+x+1\right)\)
\(=x^3\left(x^2+x+1\right)+\left(x^2+x+1\right)\)
\(=\left(x^3+1\right)\left(x^2+x+1\right)\)
\(=\left(x+1\right)\left(x^2-x+1\right)\left(x^2+x+1\right)\)
Ta có: \(x^5+x^4+x^3+x^2+x+1\)
\(=x^4\left(x+1\right)+x^2\left(x+1\right)+\left(x+1\right)\)
\(=\left(x+1\right)\left(x^4+x^2+1\right)\)
\(=\left(x+1\right)\left(x^4+2x^2+1-x^2\right)\)
\(=\left(x+1\right)\left\lbrack\left(x^2+1\right)^2-x^2\right\rbrack=\left(x+1\right)\left(x^2-x+1\right)\left(x^2+x+1\right)\)
