
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 4:
a) (2x)2-2.2x.(3/2)+(3/2)2=(2x-3/2)2
b) 4(x2+2x+1)-12x-3=4x2-4x+1=(2x)2-2.2x.1+12=(2x-1)2
c) (5x)2-2.5x.2y+(2y)2=(5x-2y)2
Bài 5:
a) (x+3)3
b)[ \(\left[\left(\sqrt{3}x\right)+2\right]^3\)]
c) (3x+31)3
d) \(\left[x+\sqrt{2}y\right]^3\)

Ta có: \(5x^2+5y^2+8xy-2x+2y+2=0\)
=>\(4x^2+8xy+4y^2+x^2-2x+1+y^2+2y+1=0\)
=>\(4\left(x^2+2xy+y^2\right)+\left(x-1\right)^2+\left(y+1\right)^2=0\)
=>\(4\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\)
=>\(\begin{cases}x+y=0\\ x-1=0\\ y+1=0\end{cases}\Rightarrow\begin{cases}x=1\\ y=-1\end{cases}\)
Khi x=1;y=-1 thì ta có:
\(M=\left(1-1\right)^{2023}+\left(1-2\right)^{2024}+\left(-1+1\right)^{2025}\)
=1

bài 13:
a: Xét tứ giác AMHN có \(\hat{AMH}=\hat{ANH}=\hat{MAN}=90^0\)
nên AMHN là hình chữ nhật
b: Xét ΔAMH vuông tại M và ΔAMD vuông tại M có
AM chung
MH=MD
Do đó: ΔAMH=ΔAMD
=>\(\hat{MAH}=\hat{MAD}\)
=>AM là phân giác của góc HAD
=>\(\hat{HAD}=2\cdot\hat{HAM}\)
Xét ΔANH vuông tại N và ΔANE vuông tại N có
AN chung
NH=NE
Do đó: ΔANH=ΔANE
=>\(\hat{NAH}=\hat{NAE}\)
=>AN là phân giác của góc HAE
=>\(\hat{HAE}=2\cdot\hat{HAN}\)
Ta có: \(\hat{DAE}=\hat{DAH}+\hat{EAH}\)
\(=2\left(\hat{HAN}+\hat{HAM}\right)=2\cdot\hat{NAM}=180^0\)
=>D,A,E thẳng hàng
c: ΔAHM=ΔADM
=>AH=AD
ΔANH=ΔANE
=>AH=AE
Xét ΔAHB và ΔADB có
AH=AD
\(\hat{HAB}=\hat{DAB}\)
AB chung
Do đó: ΔAHB=ΔADB
=>\(\hat{AHB}=\hat{ADB}\)
=>\(\hat{ADB}=90^0\)
=>BD⊥AD
=>BD⊥ DE(2)
Xét ΔAHC và ΔAEC có
AH=AE
\(\hat{HAC}=\hat{EAC}\)
AC chung
Do đó: ΔAHC=ΔAEC
=>\(\hat{AHC}=\hat{AEC}\)
=>\(\hat{AEC}=90^0\)
=>CE⊥ DE(1)
Từ (1),(2) suy ra BD//CE
=>BDEC là hình thang
d: Xét ΔHED có
N,M lần lượt là trung điểm của HE,HD
=>NM là đường trung bình của ΔHED
=>ED=2MN=MN+AH
Bài 12:
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
Hình bình hành ABDC có \(\hat{BAC}=90^0\)
nên ABDC là hình chữ nhật
b: ABDC là hình chữ nhật
=>AB//DC và AB=DC
AB//DC
=>DC//BE
ta có: AB=DC
AB=BE
Do đó: DC=BE
Xét tứ giác BCDE có
BE//DC
BE=DC
Do đó: BCDE là hình bình hành
c: DK=2BK
DK+BK=DB
Do đó: DB=2BK+BK=3BK
=>\(\frac{DK}{DB}=\frac23\)
Xét ΔADE có
DB là đường trung tuyến
\(DK=\frac23DB\)
Do đó: K là trọng tâm của ΔADE
Xét ΔADE có
K là trọng tâm
M là trung điểm của AD
Do đó: E,K,M thẳng hàng
=>EK,AD,BC đồng quy
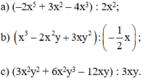


 giúp mình vs!!!
giúp mình vs!!!


a) (–2x5 + 3x2 – 4x3) : 2x2
= (–2x5) : 2x2 + 3x2 : 2x2 + (–4x3) : 2x2
= [(–2) : 2].(x5 : x2) + (3 : 2).(x2 : x2) + [(–4) : 2].(x3 : x2)
c) (3x2y2 + 6x2y3 – 12xy) : 3xy
= (3x2y2 : 3xy) + (6x2y3 : 3xy) + ( –12xy : 3xy)
= (3 : 3).(x2 : x).(y2 : y) + (6 : 3).(x2 : x).(y3 : y) + (–12 : 3).(x : x).(y : y)
= 1.x.y + 2.xy2 + (–4).1.1
= xy + 2xy2 – 4