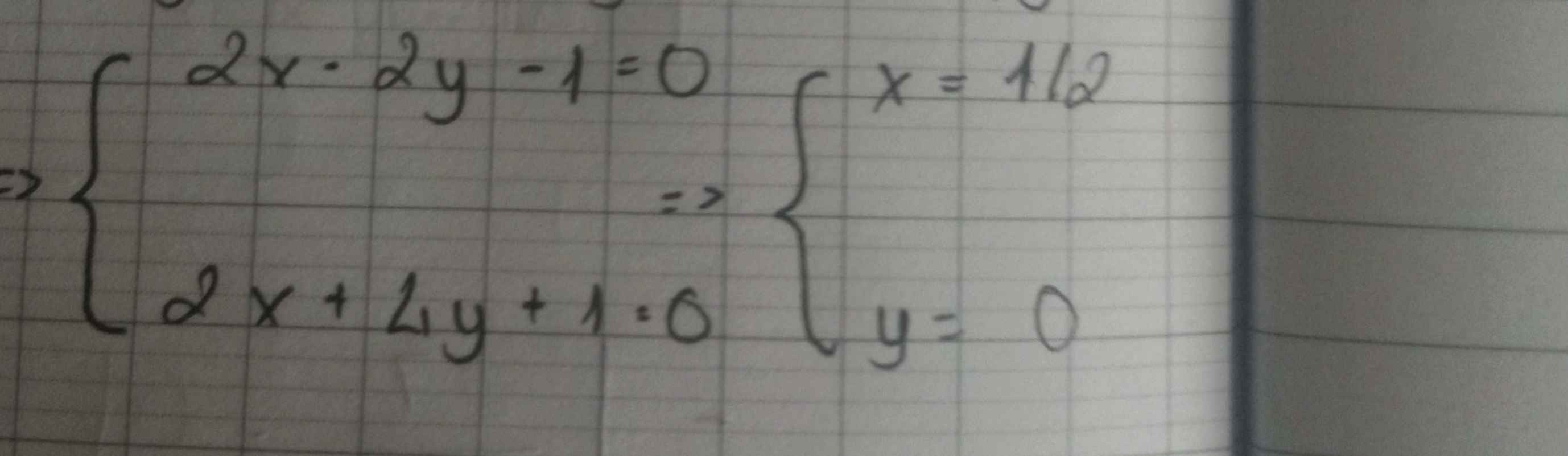Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Với \(x=0\) ko phải nghiệm
Với \(x\ne0\) chia 2 vế cho \(x^2\) ta được:
\(x^2+\dfrac{1}{x^2}+3x+\dfrac{3}{x}+m=0\)
\(\Leftrightarrow\left(x+\dfrac{1}{x}\right)^2+3\left(x+\dfrac{1}{x}\right)+m-2=0\) (1)
Đặt \(x+\dfrac{1}{x}=t\Rightarrow x^2-tx+1=0\) (2)
(2) có 2 nghiệm pb khi và chỉ khi:
\(\Delta=t^2-4>0\Rightarrow\left[{}\begin{matrix}t>2\\t< -2\end{matrix}\right.\)
Khi đó (1) trở thành:
\(t^2+3t+m-2=0\) (3)
Pt đã cho có 4 nghiệm pb khi và chỉ khi (3) có 2 nghiệm pb thỏa mãn \(\left[{}\begin{matrix}t>2\\t< -2\end{matrix}\right.\)
(3) \(\Leftrightarrow t^2+3t-2=-m\)
Đặt \(f\left(t\right)=t^2+3t-2\)
\(f\left(-2\right)=-4\) ; \(f\left(2\right)=8\)
Đồ thị hàm \(f\left(t\right)\):
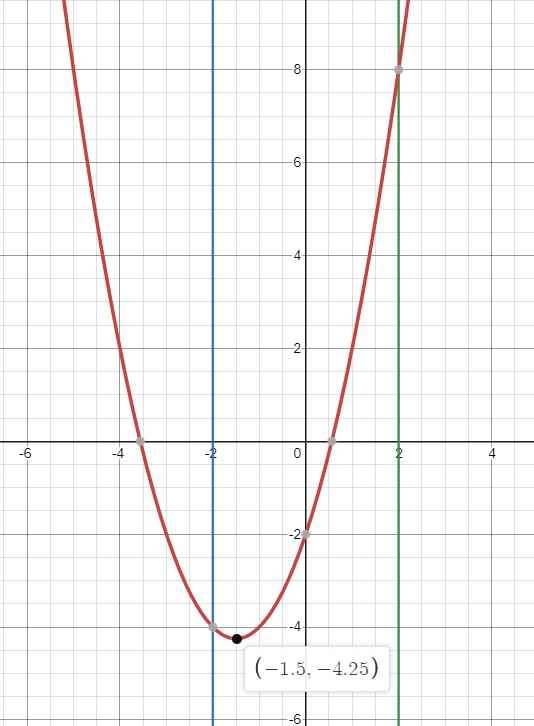
Từ đồ thị ta thấy \(y=-m\) cắt \(y=f\left(t\right)\) tại 2 điểm đều nằm ngoài \(\left[-2;2\right]\) khi và chỉ khi:
\(\left[{}\begin{matrix}-\dfrac{17}{4}< -m< -4\\-m>8\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}4< m< \dfrac{17}{4}\\m< -8\end{matrix}\right.\)
thầy cho em hỏi làm mấy dạng tìm điều kiện này thạo thì nên học qua tư liệu nào ? Thầy có thể cho e một số file chuyên đề về mấy dạng này đc không?

Đầu tiên, hãy để cả hai đồng hồ cát cùng chảy
Sau khi đồng hồ 7 phút chảy hết, lật ngược lại và bắt đầu luộc trứng.
Lúc này, chiếc đồng hồ lớn sẽ còn 11 - 7 = 4 phút. Giờ hãy đợi đồng hồ lớn chảy hết cát và lật ngược lại, bạn sẽ có một khoảng thời gian chính xác là 11 + 4 = 15 phút.

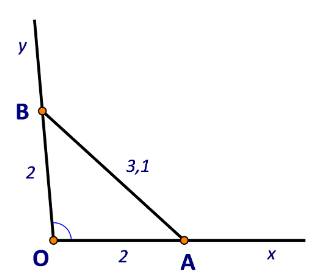
Áp dụng định lí cosin trong tam giác OAB, ta có:
\(\begin{array}{l}\cos O = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}} = \frac{{{2^2} + {2^2} - 3,{1^2}}}{{2.2.2}} \approx - 0,2\\ \Rightarrow \widehat {xOy} \approx {102^o}\end{array}\)

=>2x-2y=1 và 2x+2y=-1
=>4x=0 và x-y=1/2
=>x=0 và y=0-1/2=-1/2
Có cách bấm máy tính 570vn plus không ạ em cần biết cách bấm máy tính ạ

Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=2\\-3a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=\dfrac{3}{2}\end{matrix}\right.\)

Ấn vào.đăng nhập Gmail hoặc iCloud .nhập mật khẩu .thế là xong