Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chu kì T = 4s suy ra: \(\omega=2\pi/T=\pi/2(rad/s)\)
Biên độ A1 = 3cm, ban đầu dao động (1) qua VTCB theo chiều dương, suy ra:
\(x_1=3\cos(\dfrac{\pi}{2}t-\dfrac{\pi}{2})\)
Biên độ A2 = 2cm, ban đầu dao động (2) qua VTCB theo chiều âm, suy ra:
\(x_2=2\cos(\dfrac{\pi}{2}t+\dfrac{\pi}{2})\)
Dao động tổng hợp:
\(x=x_1+x_2=\cos(\dfrac{\pi}{2}t-\dfrac{\pi}{2})\) (cm)

Có: \(L=CR^2=Cr^2\Rightarrow R^2=r^2=Z_LZ_C,URC=\sqrt{3U}_{Lr}\Leftrightarrow Z^2_{RC}=3Z^2_{Lr}\Leftrightarrow R^2+Z^2_C=3\left(Z^2_L+R^2\right)\)
\(\Leftrightarrow-3Z^2_L+Z^2_C=2R^2\) (*) \(R^2=Z_LZ_C\) (**)
Từ (*) và (**) có: \(Z_L=\frac{R}{\sqrt{3}};Z_C=\sqrt{3}R\Rightarrow Z=\sqrt{\left(R+r\right)^2Z^2_{LC}}=\frac{4R}{\sqrt{3}}\Rightarrow\cos\phi=\frac{R+r}{Z}=\frac{\sqrt{3}}{2}\approx0,866\)
A đúng

Ta có:
Con lắc thực hiện 100 dao động hết 31,4 (s)
Lại có gốc thời gian là lúc quả cầu có li độ 2cm và đang chuyển động theo chiều dương của trục tọa độ với vận tốc có độ lớn
và

Bạn biểu diễn lại bằng véc tơ quay nhé.
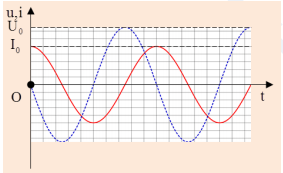
Từ đồ thị ta thấy tại thời điểm ban đầu (t=0) thì cường độ dòng điện cực đại. Còn điện áp u = 0 và đang giảm.
Ta có giản đồ véc tơ như sau:
> u, i Uo I0 > ^ O M N
Cường độ dòng điện được biểu diễn bằng véc tơ OM, điện áp được biểu diễn bằng véc tơ ON.
Từ giản đồ ta thấy u sớm pha hơn i (sớm pha \(\dfrac{\pi}{2}\) rad)