
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

Em thấy bạn Vuông nói đúng
Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.
Ví dụ:

\(\widehat {{O_1}} = \widehat {{O_2}}\) nhưng hai góc này không đối đỉnh

\(5x=3y\Rightarrow x=\dfrac{3y}{5}\)
Thay \(x=\dfrac{3y}{5}\) vào biểu thức \(x^2-y^2=-4\) ta có:
\(\left(\dfrac{3y}{5}\right)^2-y^2=-4\)
\(\dfrac{9y^2}{25}-y^2=-4\)
\(-\dfrac{16}{25}y^2=-4\)
\(y^2=-\dfrac{4}{\dfrac{-16}{25}}\)
\(y^2=\dfrac{25}{4}\)
\(\Rightarrow y=-\dfrac{5}{2};y=\dfrac{5}{2}\)
*) \(y=-\dfrac{5}{2}\Rightarrow x=\dfrac{3.\left(-\dfrac{5}{2}\right)}{5}=-\dfrac{3}{2}\)
*) \(y=\dfrac{5}{2}\Rightarrow x=\dfrac{3.\dfrac{5}{2}}{5}=\dfrac{3}{2}\)
Vậy ta được các cặp giá trị \(\left(x;y\right)\) thỏa mãn:
\(\left(-\dfrac{3}{2};-\dfrac{5}{2}\right);\left(\dfrac{3}{2};\dfrac{5}{2}\right)\)

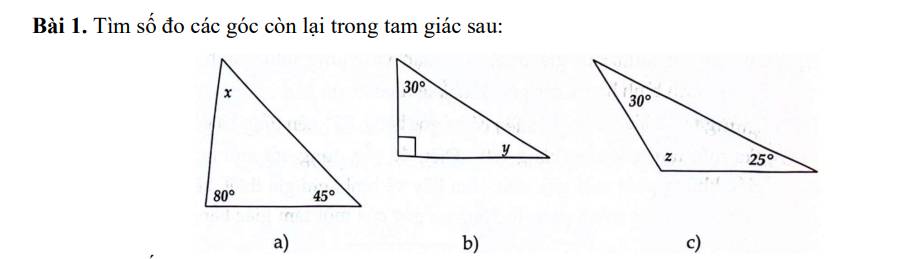
Lời giải:
Áp dụng tính chất tổng 3 góc trong một tam giác bằng $180^0$
a.
$x=180^0-80^0-45^0=55^0$
b.
$y=180^0-30^0-90^0=60^0$
c.
$z=180^0-30^0-25^0=125^0$

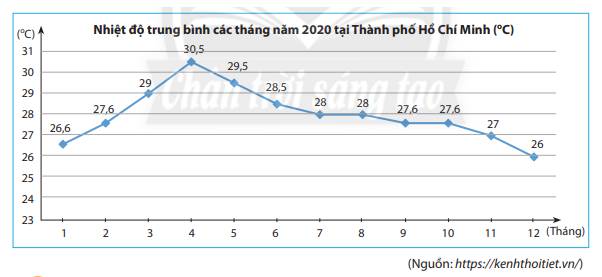
+ Biểu đồ biểu diễn nhiệt độ trung bình các tháng năm 2020 tại Thành phố Hồ Chí Minh.
+ Đơn vị thời gian là tháng, đơn vị số liệu là độ C.
+ Tháng 4 có nhiệt độ trung bình cao nhất.
+ Tháng 12 có nhiệt độ trung bình thấp nhất.
+ Nhiệt độ trung bình tăng trong những khoảng thời gian từ tháng: 1 – 2; 2 – 3; 3 – 4.
+ Nhiệt độ trung bình giảm trong những khoảng thời gian từ tháng: 4 – 5; 5 – 6; 6 – 7; 8 – 9; 10 – 11; 11 – 12.
+ Nhiệt độ trung bình không đổi trong những khoảng thời gian từ tháng: 7 – 8; 9 – 10.
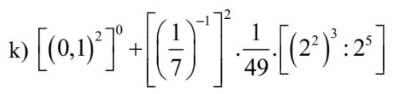


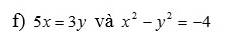
\(\left[\left(0,1\right)^2\right]^0+\left[\left(\dfrac{1}{7}\right)^{-1}\right]^2\cdot\dfrac{1}{49}\cdot\left[\left(2^2\right)^3:2^5\right]\)
\(=1+7^2\cdot\dfrac{1}{49}\cdot\left(2^6:2^5\right)\)
\(=1+49\cdot\dfrac{1}{49}\cdot2\)
\(=1+1\cdot2\)
\(=3\)
cảm ơn ạ