
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trả lời :
1 + 3 + 4 + 6 + 7 + ( -6 ) + 8 + 3 + ( -6 ) = 30
~ Hok tốt ~



Bài 4:
a) Vì $ABC$ cân tại $A$ nên $AB=AC$ và $\widehat{ABC}=\widehat{ACB}$
$\Rightarrow 180^0-\widehat{ABC}=180^0-\widehat{ACB}$
hay $\widehat{ABQ}=\widehat{ACR}$
Xét tam giác $ABQ$ và $ACR$ có:
$AB=AC$ (cmt)
$\widehat{ABQ}=\widehat{ACR}$ (cmt)
$BQ=CR$ (gt)
$\Rightarrow \triangle ABQ=\triangle ACR$ (c.g.c)
$\Rightarrow AQ=AR$
b)
$H$ là trung điểm của $BC$ nên $HB=HC$
Mà $QB=CR nên $HB+QB=HC+CR$ hay $QH=HR$
Xét tam giác $AQH$ và $ARH$ có:
$AQ=AR$ (cmt)
$QH=RH$ (cmt)
$AH$ chung
$\Rightarrow \triangle AQH=\triangle ARH$ (c.c.c)
$\Rightarrow \widehat{QAH}=\widehat{RAH}$

Em chia nhỏ bài ra mỗi bài đăng 1 lượt hỏi nha!
Bài 6:
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
=>AM⊥DE

1.
Nếu \(a+b+c=0\Rightarrow B=\dfrac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}=\dfrac{\left(-c\right)\left(-a\right)\left(-b\right)}{abc}=-1\)
Theo tính chất dãy tỉ số bằng nhau:
\(\dfrac{a+b-2017c}{c}=\dfrac{b+c-2017a}{a}=\dfrac{c+a-2017b}{b}=\dfrac{a+b-2017c+b+c-2017a+c+a-2017b}{c+a+b}\)
\(=\dfrac{-2015\left(a+b+c\right)}{a+b+c}=-2015\)
\(\Rightarrow\left\{{}\begin{matrix}a+b-2017c=-2015c\\a+c-2017b=-2015b\\b+c-2017a=-2015a\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=2c\\a+c=2b\\b+c=2a\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=2c-b\\a=2b-c\\b+c=2a\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2c-b=2b-c\\b+c=2a\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}3b=3c\\b+c=2a\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}b=c\\b+c=2a\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=c\\b=a\end{matrix}\right.\)
\(\Rightarrow a=b=c\)
Do đó:
\(B=\left(1+\dfrac{a}{a}\right)\left(1+\dfrac{a}{a}\right)\left(1+\dfrac{a}{a}\right)=2.2.2=8\)
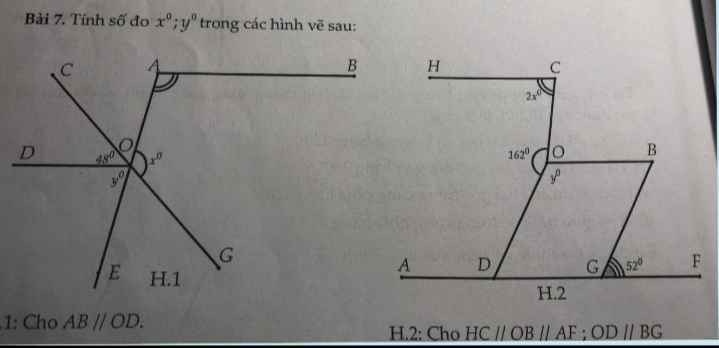

 Mọi người làm hộ mình bài 4,5,6 hộ mk cái nha...Mình cảm ơn các bạn rất nhiều
Mọi người làm hộ mình bài 4,5,6 hộ mk cái nha...Mình cảm ơn các bạn rất nhiều



Làm cái gì?