H
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Mọi người làm hộ mình bài 4,5,6 hộ mk cái nha...Mình cảm ơn các bạn rất nhiều
AH
Akai Haruma
Giáo viên
17 tháng 2 2021
Bài 4:
a) Vì $ABC$ cân tại $A$ nên $AB=AC$ và $\widehat{ABC}=\widehat{ACB}$
$\Rightarrow 180^0-\widehat{ABC}=180^0-\widehat{ACB}$
hay $\widehat{ABQ}=\widehat{ACR}$
Xét tam giác $ABQ$ và $ACR$ có:
$AB=AC$ (cmt)
$\widehat{ABQ}=\widehat{ACR}$ (cmt)
$BQ=CR$ (gt)
$\Rightarrow \triangle ABQ=\triangle ACR$ (c.g.c)
$\Rightarrow AQ=AR$
b)
$H$ là trung điểm của $BC$ nên $HB=HC$
Mà $QB=CR nên $HB+QB=HC+CR$ hay $QH=HR$
Xét tam giác $AQH$ và $ARH$ có:
$AQ=AR$ (cmt)
$QH=RH$ (cmt)
$AH$ chung
$\Rightarrow \triangle AQH=\triangle ARH$ (c.c.c)
$\Rightarrow \widehat{QAH}=\widehat{RAH}$
I
5 tháng 10 2018
mình trả lời theo ý hiểu thôi nhé , tại quên mất rồi . di dân tự do hay còn gọi là di dân bất hợp pháp , không có sự cho phép của nhà nước , ví dụ : sau chiến tranh có thể có hiện tượng " di tản " , " vượt biên trái phép " của người dân ở nước có chiến tranh
di dân có kế hoạch là di dân có tổ chức , nhà nước và các cấp chính quyền có thẩm quyền hoặc có cơ quan chuyên trách về di dân đóng vai trò và chủ động theo kế hoạch thống nhất.
vd : di cư để giãn dân số ở các thành phố lớn , di dân để tạo ra những khu kinh tế mới ,....
NL
1
TP
13 tháng 8 2017
Ta có:
\(\frac{x}{4}=\frac{y}{12}=\frac{z}{15}\) và \(y-x=4\)
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\frac{x}{4}=\frac{y}{12}=\frac{z}{15}=\frac{y-x}{12-4}=\frac{4}{8}=\frac{1}{2}\)
\(\hept{\begin{cases}\frac{x}{4}=\frac{1}{2}\Rightarrow x=\frac{1}{2}.4=2\\\frac{y}{8}=\frac{1}{2}\Rightarrow y=\frac{1}{2}.8=4\\\frac{z}{15}=\frac{1}{2}\Rightarrow z=\frac{1}{2}.15=7,5\end{cases}}\)
Vậy \(x=2;y=4;z=7,5\)
LH
20 tháng 7 2021
Ta có: 2a = 3b \(\Rightarrow\frac{a}{3}=\frac{b}{2}\) \(\Rightarrow\frac{a}{9}=\frac{b}{6}\)
4b = 3c \(\Rightarrow\frac{b}{3}=\frac{c}{4}\) \(\Rightarrow\frac{b}{6}=\frac{c}{8}\)
\(\Rightarrow\frac{a}{9}=\frac{b}{6}=\frac{c}{8}=\frac{a+b+c}{9+6+8}=\frac{46}{23}=2\)
\(\Rightarrow a=2.9=18;b=2.6=12;c=2.8=16\)
Vậy a = 18; b = 12; c = 2+
P
1
TC
7 tháng 2 2020
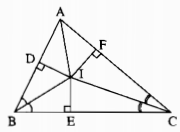
Kẻ: ID⊥AB,IE⊥BC,IF⊥ACID⊥AB,IE⊥BC,IF⊥AC
Xét hai tam giác vuông IDB và IEB, ta có:
\(\eqalign{
& \widehat {I{\rm{D}}B} = \widehat {IEB} = 90^\circ \cr
& \widehat {DBI} = \widehat {EBI}\left( {gt} \right) \cr} \)
BI cạnh huyền chung
⇒⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng)
Quảng cáo
Xét hai tam giác vuông IEC và IFC, ta có ;
\(\eqalign{
& \widehat {IEC} = \widehat {IFC} = 90^\circ \cr
& \widehat {ECI} = \widehat {FCI}\left( {gt} \right) \cr} \)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
ˆIDA=ˆIFA=90∘IDA^=IFA^=90∘
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra: ˆDAI=ˆFAIDAI^=FAI^ (hai góc tương ứng)
Vậy AI là tia phân giác của ˆA
H
7 tháng 2 2020
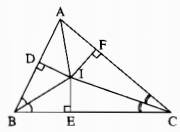
Kẻ: ID⊥AB,IE⊥BC,IF⊥ACID⊥AB,IE⊥BC,IF⊥AC
Xét hai tam giác vuông IDB và IEB, ta có:
ˆIDB=ˆIEB=90∘ˆDBI=ˆEBI(gt)IDB^=IEB^=90∘DBI^=EBI^(gt)
BI cạnh huyền chung
⇒⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng) (1)
Xét hai tam giác vuông IEC và IFC, ta có ;
ˆIEC=ˆIFC=90∘ˆECI=ˆFCI(gt)IEC^=IFC^=90∘ECI^=FCI^(gt)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
ˆIDA=ˆIFA=90∘IDA^=IFA^=90∘
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra: ˆDAI=ˆFAIDAI^=FAI^ (hai góc tương ứng)
Vậy AI là tia phân giác của ˆA
Read more: https://sachbaitap.com/cau-100-trang-151-sach-bai-tap-sbt-toan-lop-7-tap-1-c7a10140.html#ixzz6DFwdbF2W
HH
1
AD
30 tháng 7 2021
\(\frac{x}{-4}=-\frac{25}{x}\)
\(\Leftrightarrow x^2=100\)
\(\Leftrightarrow x=\pm10\)
#H