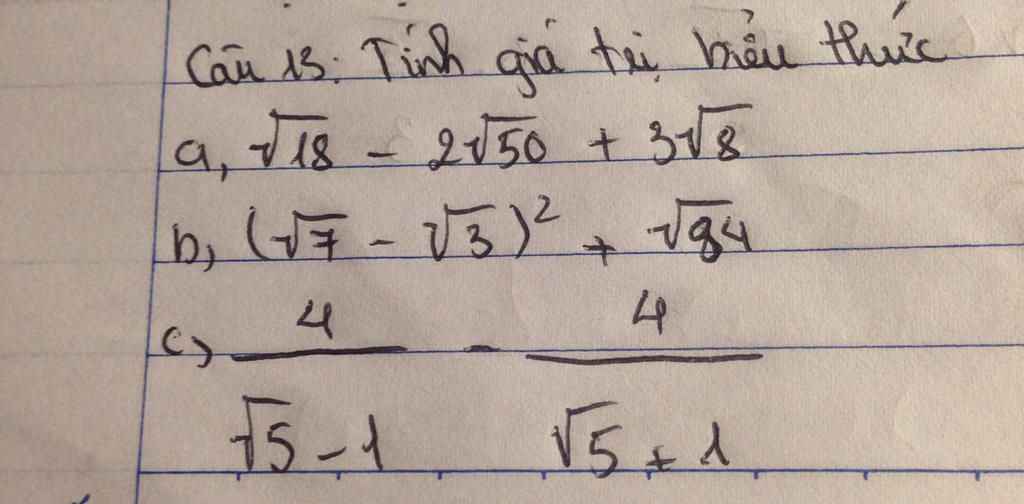K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
7 tháng 10 2021
Lời giải:
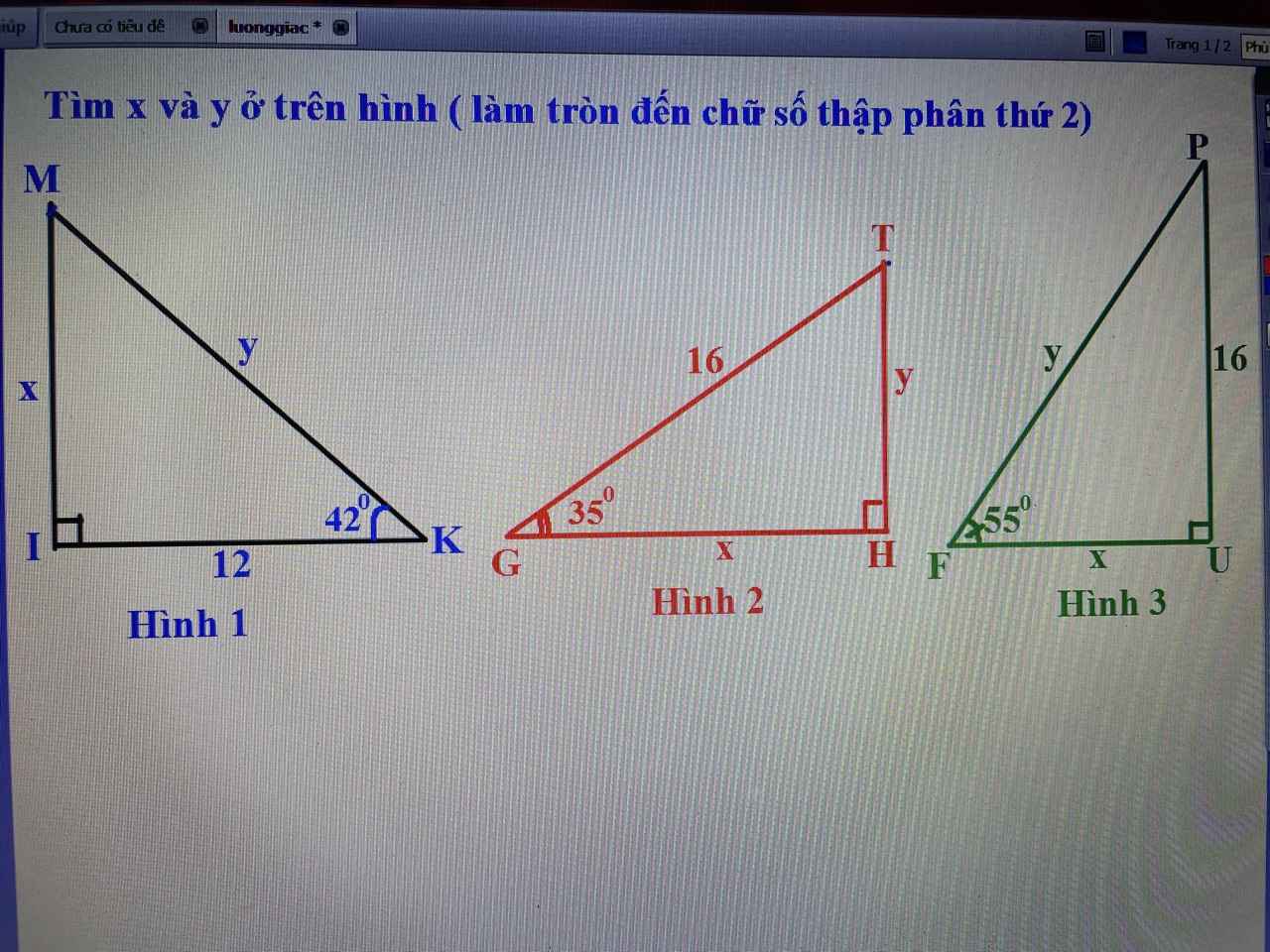
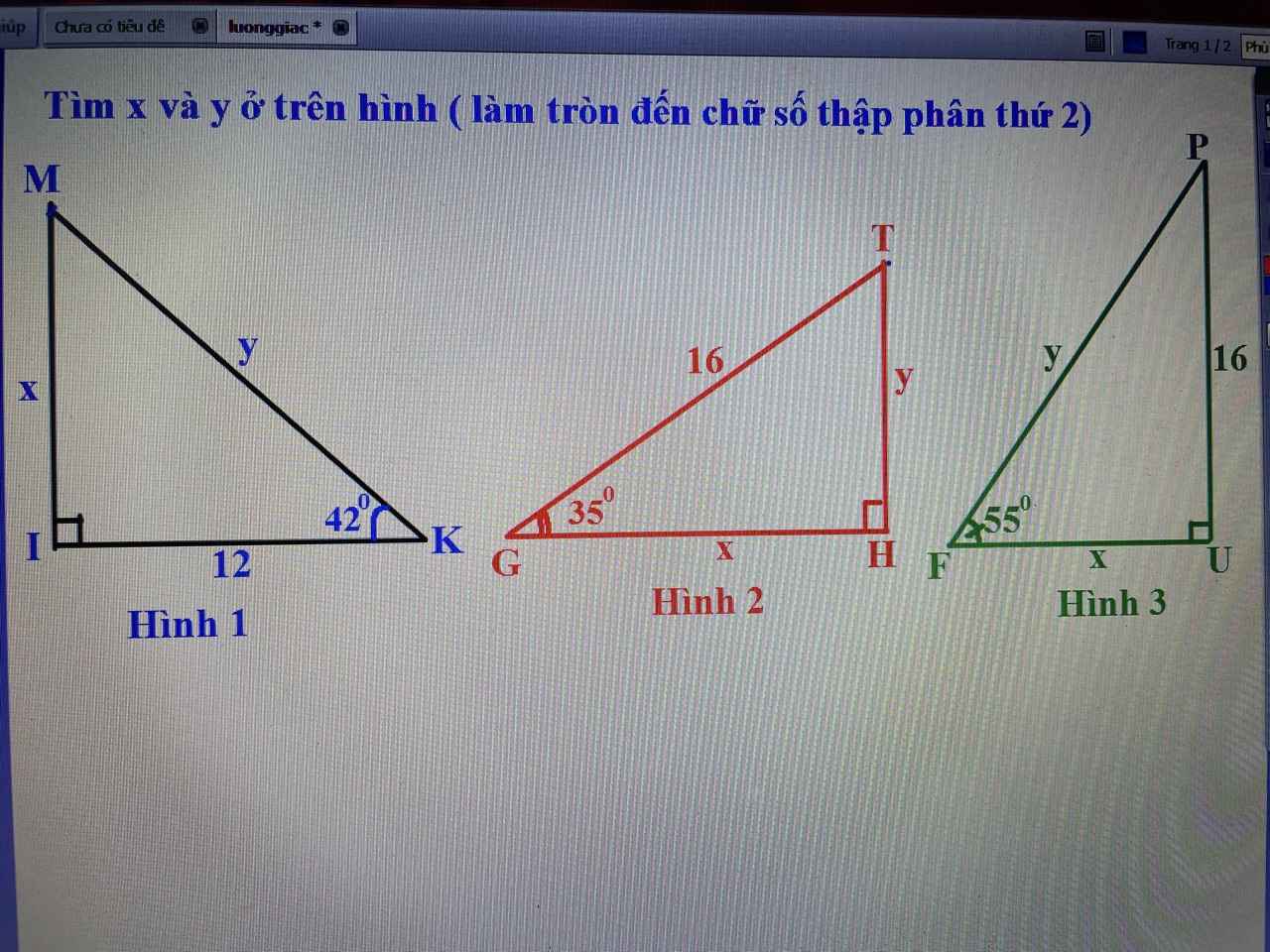
Hình 1:
$\tan K=\frac{x}{12}\Rightarrow x=12.\tan K=12.\tan 42^0=10,80$
$\cos K=\frac{12}{y}\Rightarrow y=\frac{12}{\cos K}=\frac{12}{\cos 42^0}=16,15$
Hình 2:
$\cos G=\frac{x}{16}\Rightarrow x=16\cos G=16\cos 35^0=13,11$
$\sin G=\frac{y}{16}\Rightarrow y=16\sin G=16\sin 35^0=9,18$
Hình 3:
$\tan F=\frac{16}{x}$
$\Rightarrow x=\frac{16}{\tan F}=\frac{16}{\tan 55^0}=11,20$
$\sin F=\frac{16}{y}\Rightarrow y=\frac{16}{\sin F}=\frac{16}{\sin 55^0}=19,53$
TN
3
6 tháng 10 2021
Hình 1:
Áp dụng tslg:
\(cosK=\dfrac{IK}{MK}\)\(\Rightarrow cos42^0=\dfrac{12}{y}\Rightarrow y\approx16,15\)
\(tanK=\dfrac{IM}{IK}\Rightarrow tan42^0=\dfrac{x}{12}\Rightarrow x\approx10,8\)
Hình 2:
\(sinG=\dfrac{HT}{GT}\Rightarrow sin35^0=\dfrac{y}{16}\Rightarrow y\approx9,18\)
\(cosG=\dfrac{GH}{GT}\Rightarrow cos35^0=\dfrac{x}{16}\Rightarrow x\approx10,11\)
6 tháng 10 2021
Hình 1:
\(x=12\cdot\tan42^0\simeq10.8\left(cm\right)\)
\(y=\sqrt{10.8^2+12^2}\simeq16,14\left(cm\right)\)
2 tháng 11 2021
\(a,=3\sqrt{2}-10\sqrt{2}+6\sqrt{2}=-\sqrt{2}\\ b,=10-2\sqrt{21}+2\sqrt{21}=10\\ c,=\dfrac{4\sqrt{5}+4-4\sqrt{5}+4}{\left(\sqrt{5}-1\right)\left(\sqrt{5}+1\right)}=\dfrac{8}{4}=2\)
A
0
A
1
MB
3
20 tháng 10 2021
Câu 12.
\(5\sqrt{a}+6\sqrt{\dfrac{a}{4}}-a\sqrt{\dfrac{4}{a}}+5\sqrt{\dfrac{4a}{25}}\)
\(=5\sqrt{a}+6\dfrac{\sqrt{a}}{2}-a\cdot\dfrac{2}{\sqrt{a}}+5\dfrac{2\sqrt{a}}{5}\)
\(=5\sqrt{a}+3\sqrt{a}-2\sqrt{a}+2\sqrt{a}\) (vì a>0)
\(=8\sqrt{a}\)
A
1
A
0
A
1
16 tháng 1 2022
a: Để phương trình có hai nghiệm phân biệt thì
\(1^2-4\cdot1\left(m-2\right)>0\)
=>4(m-2)<1
=>m-2<1/4
hay m<9/4
b: \(\Leftrightarrow3^2-4\cdot\left(-2\right)\left(m-3\right)>0\)
=>9+8(m-3)>0
=>9+8m-24>0
=>8m-15>0
hay m>15/8